8.2 Manager/Worker Example
8.2 Manager/Worker Example
We now begin a series of examples illustrating approaches to parallel computations that accomplish useful work. While each parallel application is unique, a number of paradigms have emerged as widely applicable, and many parallel algorithms are variations on these patterns.
One of the most universal is the "manager/worker" or "task parallelism" approach. The idea is that the work that needs to be done can be divided by a "manager" into separate pieces and the pieces can be assigned to individual "worker" processes. Thus the manager executes a different algorithm from that of the workers, but all of the workers execute the same algorithm. Most implementations of MPI (including MPICH2) allow MPI processes to be running different programs (executable files), but it is often convenient (and in some cases required) to combine the manager and worker code into a single program with the structure shown in Figure 8.5.
#include "mpi.h"
int main( int argc, char *argv[] )
{
int numprocs, myrank;
MPI_Init( &argc, &argv );
MPI_Comm_size( MPI_COMM_WORLD, &numprocs );
MPI_Comm_rank( MPI_COMM_WORLD, &myrank );
if ( myrank == 0 ) /* manager process */
manager_code ( numprocs );
else /* worker process */
worker_code ( );
MPI_Finalize( );
return 0;
}
Figure 8.5: Framework of the matrix-vector multiply program.
Sometimes the work can be evenly divided into exactly as many pieces as there are workers, but a more flexible approach is to have the manager keep a pool of units of work larger than the number of workers and assign new work dynamically to workers as they complete their tasks and send their results back to the manager. This approach, called self-scheduling, works well in the presence of tasks of varying sizes or workers of varying speeds.
We illustrate this technique with a parallel program to multiply a matrix by a vector. (A Fortran version of this same program can be found in [48].) This program is not a particularly good way to carry out this operation, but it illustrates the approach and is simple enough to be shown in its entirety. The program multiplies a square matrix a by a vector b and stores the result in c. The units of work are the individual dot products of the rows of a with the vector b. Thus the manager, code for which is shown in Figure 8.6, starts by initializing a. The manager then sends out initial units of work, one row to each worker. We use the MPI tag on each such message to encode the row number we are sending. Since row numbers start at 0 but we wish to reserve 0 as a tag with the special meaning of "no more work to do," we set the tag to one greater than the row number. When a worker sends back a dot product, we store it in the appropriate place in c and send that worker another row to work on. Once all the rows have been assigned, workers completing a task are sent a "no more work" message, indicated by a message with tag 0.
#define SIZE 1000
#define MIN( x, y ) ((x) < (y) ? x : y)
void manager_code( int numprocs )
{
double a[SIZE][SIZE], c[SIZE];
int i, j, sender, row, numsent = 0;
double dotp;
MPI_Status status;
/* (arbitrary) initialization of a */
for (i = 0; i < SIZE; i++ )
for ( j = 0; j < SIZE; j++ )
a[i][j] = ( double ) j;
for ( i = 1; i < MIN( numprocs, SIZE ); i++ ) {
MPI_Send( a[i-1], SIZE, MPI_DOUBLE, i, i, MPI_COMM_WORLD );
numsent++;
}
/* receive dot products back from workers */
for ( i = 0; i < SIZE; i++ ) {
MPI_Recv( &dotp, 1, MPI_DOUBLE, MPI_ANY_SOURCE, MPI_ANY_TAG,
MPI_COMM_WORLD, &status );
sender = status.MPI_SOURCE;
row = status.MPI_TAG - 1;
c[row] = dotp;
/* send another row back to this worker if there is one */
if ( numsent < SIZE ) {
MPI_Send( a[numsent], SIZE, MPI_DOUBLE, sender,
numsent + 1, MPI_COMM_WORLD );
numsent++;
}
else /* no more work */
MPI_Send( MPI_BOTTOM, 0, MPI_DOUBLE, sender, 0,
MPI_COMM_WORLD );
}
}
Figure 8.6: The matrix-vector multiply program, manager code.
The code for the worker part of the program is shown in Figure 8.7. A worker initializes b, receives a row of a in a message, computes the dot product of that row and the vector b, and then returns the answer to the manager, again using the tag to identify the row. A worker repeats this until it receives the "no more work" message, identified by its tag of 0.
void worker_code( void )
{
double b[SIZE], c[SIZE];
int i, row, myrank;
double dotp;
MPI_Status status;
for ( i = 0; i < SIZE; i++ ) /* (arbitrary) b initialization */
b[i] = 1.0;
MPI_Comm_rank( MPI_COMM_WORLD, &myrank );
if ( myrank <= SIZE ) {
MPI_Recv( c, SIZE, MPI_DOUBLE, 0, MPI_ANY_TAG,
MPI_COMM_WORLD, &status );
while ( status.MPI_TAG > 0 ) {
row = status.MPI_TAG - 1;
dotp = 0.0;
for ( i = 0; i < SIZE; i++ )
dotp += c[i] * b[i];
MPI_Send( &dotp, 1, MPI_DOUBLE, 0, row + 1,
MPI_COMM_WORLD );
MPI_Recv( c, SIZE, MPI_DOUBLE, 0, MPI_ANY_TAG,
MPI_COMM_WORLD, &status );
}
}
}
Figure 8.7: The matrix-vector multiply program, worker code.
This program requires at least two processes to run: one manager and one worker. Unfortunately, adding more workers is unlikely to make the job go faster. We can analyze the cost of computation and communication mathematically and see what happens as we increase the number of workers. Increasing the number of workers will decrease the amount of computation done by each worker, and since they work in parallel, this should decrease total elapsed time. On the other hand, more workers mean more communication, and the cost of communicating a number is usually much greater than the cost of an arithmetical operation on it. The study of how the total time for a parallel algorithm is affected by changes in the number of processes, the problem size, and the speed of the processor and communication network is called scalability analysis. We analyze the matrix-vector program as a simple example.
First, let us compute the number of floating-point operations. For a matrix of size n, we have to compute n dot products, each of which requires n multiplications and n - 1 additions. Thus the number of floating-point operations is n ? (n + (n - 1)) = n?(2n-1) = 2n2-n. If Tcalc is the time it takes a processor to do one floating-point operation,[3] then the total computation time is (2n2 - n) ? Tcalc. Next, we compute the number of communications, defined as sending one floating-point number. (We ignore for this simple analysis the effect of message lengths; following Section 1.3, we could model these as s + rn, where Tcomm ≈ r.) Leaving aside the cost of communicating b (perhaps it is computed locally in a preceding step), we have to send each row of a and receive back one dot product answer. So the number of floating-point numbers communicated is (n ? n) + n = n2 + n. If Tcomm is the time to communicate one number, we get (n2 + n) ? Tcomm for the total communication time. Thus the ratio of communication time to computation time is
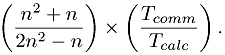
In many computations the ratio of communication to computation can be reduced almost to 0 by making the problem size larger. Our analysis shows that this is not the case here. As n gets larger, the term on the left approaches 1/2. Thus we can expect communication costs to prevent this algorithm from showing good speedups, even on large problem sizes.
The situation is better in the case of matrix-matrix multiplication, which could be carried out by a similar algorithm. We would replace the vectors b and c by matrices, send the entire matrix b to the workers at the beginning of the computation, and then hand out the rows of a as work units, just as before. The workers would compute an entire row of the product, consisting of the dot products of the row of a with all of the column of b, and then return a row of c to the manager.
Let us now do the scalability analysis for the matrix-matrix multiplication. Again we ignore the initial communication of b. The number of operations for one dot product is n + (n + 1) as before, and the total number of dot products calculated is n2. Thus the total number of operations is n2 ? (2n - 1) = 2n3 - n2. The number of numbers communicated has gone up to (n ? n) + (n ? n) = 2n2. So the ratio of communication time to computation time has become
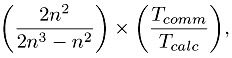
which does tend to 0 as n gets larger. Thus, for large matrices the communication costs play less of a role.
Two other difficulties with this algorithm might occur as we increase the size of the problem and the number of workers. The first is that as messages get longer, the workers waste more time waiting for the next row to arrive. A solution to this problem is to "double buffer" the distribution of work, having the manager send two rows to each worker to begin with, so that a worker always has some work to do while waiting for the next row to arrive.
Another difficulty for larger numbers of processes can be that the manager can become overloaded so that it cannot assign work in a timely manner. This problem can most easily be addressed by increasing the size of the work unit, but in some cases it is necessary to parallelize the manager task itself, with multiple managers handling subpools of work units.
A more subtle problem has to do with fairness: ensuring that all worker processes are fairly serviced by the manager. MPI provides several ways to ensure fairness; see [48, Section 7.1.4].
[3]The symbol f was used in Section 1.3; we use Tcalc here because of the more prominent role of floating point in this analysis.







