6.6 Special Rules for Special Cases
The heuristic rules so far handle most cases well and nearly always generate excellent, robust plans. However, there are some assumptions behind the rationale for these rules, which are not always true. Surprisingly often, even when the assumptions are wrong, they are right enough to yield a plan that is at least close to optimum. Here, I lay these assumptions out and examine more sophisticated rules to handle the rare cases in which deviations from the assumptions matter:
Intermediate query results in the form of Cartesian products lead to poor performance. If you do not follow the joins when working out a join order, the result is a Cartesian product between the first set of rows and the rows from the leaped-to node. Occasionally, this is harmless, but even when it is faster than a join order following the links, it is usually dangerous and scales poorly as table volumes increase.
Detail join ratios are large, much greater than 1.0. Since master join ratios (downward on the join tree) are never greater than 1.0, this makes it much safer to join downward as much as possible before joining upward, even when upward joins give access to more filters. (The filters on the higher nodes usually do not discard more rows than the database picks up going to the more detailed table.) Even when detail join ratios are small, the one-to-many nature of the join offers at least the possibility that they could be large in the future or at other sites running the same application. This tends to favor SQL that is robust for the case of a large detail join ratio, except when you have high confidence that the local, current statistics are relatively timeless and universal.
The table at the root of the join tree is significantly larger than the other tables, which serve as master tables or lookup tables to it. This assumption follows from the previous assumption. Since larger tables have poorer hit ratios in cache and since the rowcount the database reads from this largest table is often much larger than most or all other rowcounts it reads, the highest imperative in tuning the query is to minimize the rowcount read from this root detail table.
Master join ratios are either exactly 1.0 or close enough to 1.0 that the difference doesn't matter. This follows in the common case in which detail tables have nonnull foreign keys with excellent referential integrity.
When tables are big enough that efficiency matters, there will be one filter ratio that is much smaller than the others. Near-ties, two tables that have close to the same filter ratio, are rare. If the tables are large and the query result is relatively small, as useful query results almost always are, then the product of all filter ratios must be quite small. It is much easier to get this small result with one selective filter, sometimes combined with a small number of fairly unselective filters, than with a large number of comparable, semiselective filters. Coming up with a business rationale for lots of semiselective filters turns out to be difficult, and, empirically speaking, I could probably count on one hand the number of times I've seen such a case in over 10 years of SQL tuning. Given one filter that is much more selective than the rest, the way to guarantee reading the fewest rows from that most important root detail table is to drive the query from the table with that best filter.
The rowcount that the query returns, even before any possible aggregation, will be small enough that, even for tiny master tables, there is little or no incentive to replace nested loops through join keys with independent table reads followed by hash joins. Note that this assumption falls apart if you do the joins with a much higher rowcount than the query ultimately returns. However, the heuristics are designed to ensure that you almost never find a much higher rowcount at any intermediate point in the query plan than the database returns from the whole query.
The following sections add rules that handle rare special cases that go against these assumptions.
6.6.1 Safe Cartesian Products
Consider the query diagrammed in Figure 6-14. Following the usual rules (and breaking ties by choosing the leftmost node, just for consistency), you drive into the filter on T1 and join to M following the index on the foreign key pointing to T1. You then follow the primary-key index into T2, discarding in the end the rows that fail to match the filter on T2. If you assume that T1 has 100 rows, based on the join ratios M must have 100,000 rows and T2 must have 100 rows.
Figure 6-14. A query with a potentially good Cartesian-product execution plan
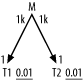
The plan just described would touch 1 row in T1, 1,000 rows in M (1% of the total), and 1,000 rows in T2 (each row in T2 10 times, on average), before discarding all but 10 rows from the result. Approximating query cost as the number of rows touched, the cost would be 2,001. However, if you broke the rules, you could get a plan that does not follow the join links. You could perform nested loops between T1 and T2, driving into their respective filter indexes. Because there is no join between T1 and T2 the result would be a Cartesian product of all rows that meet the filter condition on T1 and all rows that meet the filter condition on T2. For the table sizes given, the resulting execution plan would read just a single row from each of T1 and T2. Following the Cartesian join of T1 and T2, the database could follow an index on the foreign key that points to T1, into M, to read 1,000 rows from M. Finally, the database would discard the 990 rows that fail to meet the join condition that matches M and T2.
|
Using the Cartesian product, the plan costs just 1,002, using the rows-touched cost function.
What happens if the table sizes double? The original plan cost, following the join links, exactly doubles, to 4,002, in proportion to the number of rows the query will return, which also doubles. This is normal for robust plans, which have costs proportional to the number of rows returned. However, the Cartesian-product plan cost is less well behaved: the database reads 2 rows from T1; then, for each of those rows, reads the same 2 rows of T2 (4 rows in all); then, with a Cartesian product that has 4 rows, reads 4,000 rows from M. The query cost, 4,006, now is almost the same as the cost of the standard plan. Doubling table sizes once again, the standard plan costs 8,004, while the Cartesian-product plan costs 16,020. This demonstrates the lack of robustness in most Cartesian-product execution plans, which fail to scale well as tables grow. Even without table growth, Cartesian-product plans tend to behave less predictably than standard plans, because filter ratios are usually averages across the possible values. A filter that matches just one row on average might sometimes match 5 or 10 rows for some values of the variable. When a filter for a standard, robust plan is less selective than average, the cost will scale up proportionally with the number of rows the query returns. When a Cartesian-product plan runs into the same filter variability, its cost might scale up as the square of the filter variability, or worse.
Sometimes, though, you can have the occasional advantages of Cartesian products safely. You can create a Cartesian product of as many guaranteed-single-row sets as you like with perfect safety, with an inexpensive, one-row result. You can even combine a one-row set with a multirow set and be no worse off than if you read the multirow set in isolation from the driving table. The key advantage of robust plans is rigorous avoidance of execution plans that combine multiple multirow sets. You might recall that in Chapter 5 the rules required you to place an asterisk next to unique filter conditions (conditions guaranteed to match at most a single row). I haven't mentioned these asterisks since, but they finally come into play here.
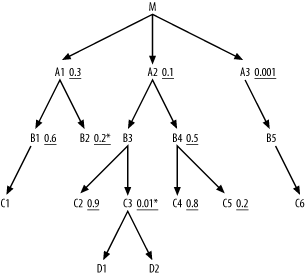
Consider Figure 6-15. Note that you find two unique filters, on B2 and C3. Starting from the single row of C3 that matches its unique filter condition, you know it will join to a single row of D1 and D2, through their primary keys, based on the downward-pointing arrows to D1 and D2. Isolate this branch, treating it as a separate, single-row query. Now, query the single row of B2 that matches its unique filter condition, and combine these two independent queries by Cartesian product for a single-row combined set.
Figure 6-15. A query with unique filter conditions
Placing these single-row queries first, you find an initial join order of (C3, D1, D2, B2) (or (B2, C3, D1, D2); it makes no difference). If you think of this initial prequeried single-row result as an independent operation, you find that tables A1 and B3 acquire new filter conditions, because you can know the values of the foreign keys that point to B2 and C3 before you perform the rest of the query. The modified query now looks like Figure 6-16, in which the already-executed single-row queries are covered by a gray cloud, showing the boundaries of the already-read portion of the query.
Figure 6-16. A query with unique filter conditions, with single-row branches preread
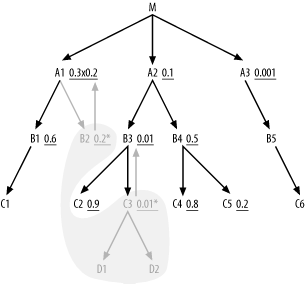
Upward-pointing arrows show that the initial filter condition on A1 combines with a new filter condition on the foreign key into B2 to reach a combined selectivity of 0.06, while the initially unfiltered node B3 acquires a filter ratio of 0.01 from its foreign-key condition, pointing into C3.
|
You can now optimize the remaining portion of the query, outside the cloud, exactly as if it stood alone, following the standard rules. You then find that A3 is the best driving table, having the best filter ratio. (It is immaterial that A3 does not join directly to B2 or C3, since a Cartesian product with the single-row set is safe.) From there, drive down to B5 and C6, then up to M. Since A1 acquired added selectivity from its inherited filter on the foreign key that points to B2, it now has a better filter ratio than A2, so join to A1 next. So far, the join order is (C3, D1, D2, B2, A3, B5, C6, M, A1), and the query, with a join cloud, looks like Figure 6-17.
Figure 6-17. A query with unique filter conditions, with single-row branches preread and a join cloud around the next five nodes read
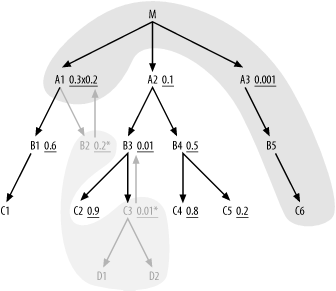
Since you preread B2, the next eligible nodes are B1 and A2, and A2 has the better filter ratio. This adds B3 and B4 to the eligible list, and you find that the inherited filter on B3 makes it the best next choice in the join order. Completing the join order, following the normal rules, you reach B4, C5, B1, C4, C2, and C1, in that order, for a complete join order of (C3, D1, D2, B2, A3, B5, C6, M, A1, A2, B3, B4, C5, B1, C4, C2, C1).
Even if you have just a single unique filter condition, follow this process of prereading that single-row node or branch, passing the filter ratio upward to the detail table above and optimizing the resulting remainder of the diagram as if the remainder of the diagram stood alone. When the unique condition is on some transaction table, not some type or status table, that unique condition will also usually yield the best filter ratio in the query. In this case, the resulting join order will be the same order you would choose if you did not know that the filter condition was unique. However, when the best filter is not the unique filter, the best join order can jump the join skeleton, which is to say that it does not reach the second table through a join key that points to the first table.
6.6.2 Detail Join Ratios Close to 1.0
Treat upward joins like downward joins when the join ratio is close to 1.0 and when this allows access to useful filters (low filter ratios) earlier in the execution plan. When in doubt, you can try both alternatives. Figure 6-18 shows a case of two of the upward joins that are no worse than downward joins. Before you look at the solution, try working it out yourself.
Figure 6-18. A case with detail joins ratios equal to 1.0
As usual, drive to the best filter, on B4, with an index, and reach the rest of the tables with nested loops to the join-key indexes. Unlike previous cases, you need not complete all downward joins before considering to join upward with a join ratio equal to 1.0.
|
As usual, look for filters in the immediately adjacent nodes first, and find that the first two best join opportunities are C5 and then C4. Next, you have only the opportunity for the upward join to unfiltered node A2, which you would do next even if the detail join ratio were large. (The low join ratio to A2 turned out not to matter.) So far, the join order is (B4, C5, C4, A2).
From the cloud around these nodes, find immediately adjacent nodes B3 (downward) and M (upward). Since the detail join ratio to M is 1.0, you need not prefer to join downward, if other factors favor M. Neither node has a filter, so look at filters on nodes adjacent to them to break the tie. The best filter ratio adjacent to M is 0.3 (on A1), while the best adjacent to B3 is 0.5 (on C2), favoring M, so join next to M and A1. The join order at this point is (B4, C5, C4, A2, M, A1). Now that the database has reached the root node, all joins are downward, so the usual rules apply for the rest of the optimization, considering immediately adjacent nodes first and considering nodes adjacent to those nodes to break ties. The complete optimum join order is (B4, C5, C4, A2, M, A1, B3, C2, B1, C1, A3, B5, C6, C3, D1, (D2, B2)).
|
Note that, even in this specially contrived case designed to show an exception to the earlier rule, you find only modest improvement for reaching A1 earlier than the simple heuristics would allow, since the improvement is relatively late in the join order.
6.6.3 Join Ratios Less than 1.0
If either the detail join ratio or the master join ratio is less than 1.0, you have, in effect, a join that is, on average, [some number]-to-[less than 1.0]. Whether the less-than-1.0 side of that join is capable of being to-many is immaterial to the optimization problem, as long as you are confident that the current average is not likely to change much on other database instances or over time. If a downward join with a normal master join ratio of 1.0 is preferred over a to-many upward join, a join that follows a join ratio of less than 1.0 in any direction is preferred even more. These join ratios that are less than 1.0 are, in a sense, hidden filters that discard rows when you perform the joins just as effectively as explicit single-node filters discard rows, so they affect the optimal join order like filters.
6.6.3.1 Rules for join ratios less than 1.0
You need three new rules to account for the effect of smaller-than-normal join ratios on choosing the optimum join order:
When choosing a driving node, all nodes on the filtered side of a join inherit the extra benefit of the hidden join filter. Specifically, if the join ratio less than 1.0 is J and the node filter ratio is R, use J x R when choosing the best node to drive the query. This has no effect when comparing nodes on the same side of a join filter, but it gives nodes on the filtered side of a join an advantage over nodes on the unfiltered side of the join.
When choosing the next node in a sequence, treat all joins with a join ratio J (a join ratio less than 1.0) like downward joins, and use J x R as the effective node filter ratio when comparing nodes, where R is the single-node filter ratio of the node reached through that filtering join.
However, for master join ratios less than 1.0, consider whether the hidden filter is better treated as an explicit foreign-key-is-not-null filter. Making the is-not-null filter explicit allows the detail table immediately above the filtering master join also to inherit the adjusted selectivity J x R for purposes of both choice of driving table and join order from above. See the following sections for more details on this rule.
6.6.3.2 Detail join ratios less than 1.0
The meaning of the small join ratio turns out to be quite different depending on whether it is the master join ratio or the detail join ratio that is less than 1.0. A detail join ratio less than 1.0 denotes the possibility of multiple details, when it is more common to have no details of that particular type than to have more than one. For example, you might have an Employees table linked to a Loans table to track loans the company makes to a few top managers as part of their compensation. The database design must allow for some employees to have multiple loans, but far more employees have no loans from the company at all, so the detail join ratio would be nearly 0. For referential integrity, the Employee_ID column in Loans must point to a real employee; that is its only purpose, and all loans in this table are to employees. However, there is no necessity at all for an Employee_ID to correspond to any loan. The Employee_ID column of Employees exists (like any primary key) to point to its own row, not to point to rows in another table, and there is no surprise when the join fails to find a match in the upward direction, pointing from primary key to foreign key.
Since handling of detail join ratios less than 1.0 turns out to be simpler, though less common, I illustrate that case first. I'll elaborate the example of the previous paragraph to try to lend some plausibility to the new rules. Beginning with a query that joins Employees to Loans, add a join to Departments, with a filter that removes half the departments. The result is shown in Figure 6-19, with each node labeled by the initial of its table.
Figure 6-19. Simple example with a filtering join
|
Let there be 1,000 employees, 10 departments, and 10 loans to 8 of those employees. Let the only filter be the filter that discards half the departments. The detail join ratio to Loans must be 0.01, since after joining 1,000 employees to the Loans table, you would find only the 10 loans. The original rules would have you drive to the only filtered table, Departments, reading 5 rows, joining to half the employees, another 500 rows, then joining to roughly half the loans (from the roughly 4 employees in the chosen half of the departments). The database would then reach 5 loans, while performing 496 unsuccessful index range scans on the Employee_ID index for Loans using Employee_IDs of employees without loans.
On the other hand, if the Loans table inherits the benefit of the filtering join, you would choose to drive from Loans, reading all 10 of them, then go to the 10 matching rows in Employees (8 different rows, with repeats to bring the total to 10). Finally, join to Departments 10 times, when the database finally discards (on average) half. Although the usual objective is to minimize rows read from the top table, this example demonstrates that minimizing reads to the table on the upper end of a strongly filtering detail join is nowhere near as important as minimizing rows read in the much larger table below it.
How good would a filter on Employees have to be to bring the rows read from Employees down to the number read in the second plan? The filter would have to be exactly as good as the filtering join ratio, 0.01. Imagine that it were even better, 0.005, and lead to just 5 employees (say, a filter on Last_Name). In that case, what table should you join next? Again, the original rules would lead you to Departments, both because it is downward and because it has the better filter ratio. However, note that from 5 employees, the database will reach, on average, just 0.05 loans, so you are much better off joining to Loans before joining to Departments.
|
6.6.3.3 Optimizing detail join ratios less than 1.0 with the rules
Figure 6-20 illustrates another example with a detail join ratio under 1.0. Try working out the join order before you read on.
Figure 6-20. Example with a detail join ratio less than 1.0
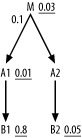
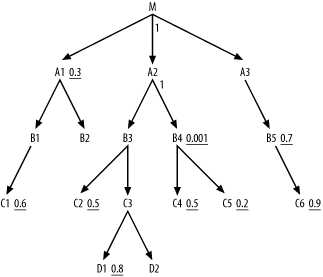
First, examine the effect of the join ratio on the choice of driving table. In Figure 6-21, I show the adjustments to filter ratios from the perspective of choosing the driving table. After these adjustments, the effective filter of 0.003 on M is best, so drive from M. From this point, revert to the original filter ratios to choose the rest of the join order, because, when driving from any node (M, A2, or B2) on the detail side of that join, this join ratio no longer applies. In a more complex query, it might seem like a lot of work to calculate all these effective filter values for many nodes on one side of a filtering join. In practice, you just find the best filter ratio on each side (0.01 for A1 and 0.03 for M, in this case) and make a single adjustment to the best filter ratio on the filtered side of the join.
Figure 6-21. Effective filters for choosing the driving table
|
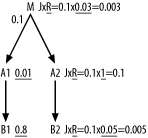
When choosing the rest of the join order, compare the original filter ratios on A1 and A2, and choose A1 next. Comparing B1 to A2, choose B1, and find the join order so far: (M, A1, B1). The rest of the join order is fully constrained by the join skeleton, for a complete join order of (M, A1, B1, A2, B2).
Figure 6-22 leads to precisely the same result. It makes no difference that this time the lowest initial filter ratio is not directly connected to the filtering join; all nodes on the filtered side of the join get the benefit of the join filter when choosing the driving table, and all nodes on the other side do not. Neither A1 nor A2 offers filters that drive from M, so choose A1 first for the better two-away filter on B1, and choose the same join order as in the last example.
Figure 6-22. Another example with a detail join ratio less than 1.0
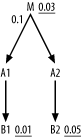
In Figure 6-23, M and B2 get the same benefit from the filtering join, so simply compare unadjusted filter ratios and choose B2. From there, the join order is fully constrained by the join skeleton: (B2, A2, M, A1, B1).
Figure 6-23. An example comparing only filters on the same side of the filtering join
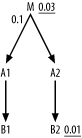
In Figure 6-24, again you compare only filtered nodes on the same side of the filtering join, but do you see an effect on later join order?
Figure 6-24. Another example comparing only filters on the same side of the filtering join
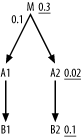
The benefit of the filtering join follows only if you follow the join in that direction. Since you drive from A2, join to M with an ordinary one-to-many join from A2, which you should postpone as long as possible. Therefore, join downward to B2 before joining upward to M, even though M has the better filter ratio. The join order is therefore (A2, B2, M, A1, B1).
Try working out the complete join order for Figure 6-25 before you read on.
Figure 6-25. One last example with a detail join ratio greater than 1.0
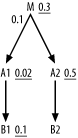
Here, note that the adjustment to filter ratios when choosing the driving table is insufficient to favor the filtered side of the join; the best filter on A2 is still favored. Where do you go from there, though? Now, the filtering join does matter. This theoretically one-to-many join is really usually one-to-zero, so, even though it is upward on the diagram, you should favor it over an ordinary downward join with a normal join ratio (unshown, by convention) of 1.0. For purposes of choosing the next table, the effective filter on M is R / J (0.3 / 0.1=0.03), better than the filter on B1, so join to M next. However, when you compare A2 and B1, compare simple, unadjusted filter ratios, because you have, in a sense, already burned the benefit of the filtering join to M. The full join order, then, is (A1, M, B1, A2, B2).
6.6.3.4 Master join ratios less than 1.0
Master join ratios less than 1.0 have two potential explanations:
The relationship to the master does not apply (or is unknown) in some cases, where the foreign key to that master is null.
The relationship to the master table is corrupt in some cases, where the nonnull foreign-key value fails to point to a legitimate master record. Since the only legitimate purpose of a foreign key is to point unambiguously to a matching master record, nonnull values of that key that fail to join to the master are failures of referential integrity. These referential-integrity failures happen in this imperfect world, but the ideal response is to fix them, either by deleting detail records that become obsolete when the application eliminates their master records, or by fixing the foreign key to point to a legitimate master or to be null. It is a mistake to change the SQL to work around a broken relationship that ought to be fixed soon, so you should generally ignore master join ratios that are less than 1.0 for such failed referential integrity.
The first case is common and legitimate for some tables. For example, if the company in the earlier Loans-table example happened to be a bank, they might want a single Loans table for all loans the bank makes, not just those to employees, and in such a Loans table Employee_ID would apply only rarely, nearly always being null. However, in this legitimate case, the database need not perform the join to pick up this valuable row-discarding hidden join filter. If the database has already reached the Loans table, it makes much more sense to make the filter explicit, with a condition Employee_ID IS NOT NULL in the query. This way, the execution engine will discard the unjoinable rows as soon as it reaches the Loans table. You can choose the next join to pick up another filter early in the execution plan, without waiting for a join to Employees.
|
In the following examples, assume that master join ratios less than 1.0 come only from sometimes-null foreign keys, not from failed referential integrity. Choose the driving table by following the rules of this section. If the driving table reaches the optional master table from above, make the is-not-null condition explicit in the query and migrate the selectivity of that condition into the detail node filter ratio. Consider the SQL diagram in Figure 6-26.
Figure 6-26. A query with a filtering master join
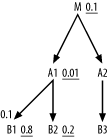
First, does the master join ratio affect the choice of driving table? Both sides of the join from A1 to B1 can see the benefit of this hidden join filter, and A1 has the better filter ratio to start with. Nodes attached below B1 would also benefit, but there are no nodes downstream of B1. No other node has a competitive filter ratio, so drive from A1 just as if there were no hidden filter. To see the best benefit of driving from A1, make explicit the is-not-null condition on A1's foreign key that points to B1, with an added clause:
A1.ForeignKeyToB1 IS NOT NULL
This explicit addition to the SQL enables the database to perform the first join to another table with just the fraction (0.01 / 0.1=0.001) of the rows in A1. If you had the column ForeignKeyToB1 in the driving index filter, the database could even avoid touching the unwanted rows in A1 at all. Where do you join next? Since the database has already picked up the hidden filter (made no longer hidden) from the now-explicit condition A1.ForeignKeyToB1 IS NOT NULL, you have burned that extra filter, so compare B1 and B2 as if there were no filtering join.
|
Comparing B1 and B2 for their simple filter ratios, choose B2 first, and choose the order (A1, B2, B1, M, A2, B3).
Now, consider the SQL diagram in Figure 6-27, and try to work it out yourself before reading further.
Figure 6-27. Another query with a filtering master join
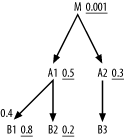
Again, the filtering join has no effect on the choice of driving table, since the filter ratio on M is so much better than even the adjusted filter ratios on A1 and B1. Where do you join next? When you join from the unfiltered side of the filtering master join, make the hidden filter explicit with an is-not-null condition on ForeignKeyToB1. When you make this filter explicit, the join of the remaining rows has an effective join ratio of just 1.0, like most master joins, and the adjusted SQL diagram looks like Figure 6-28.
Figure 6-28. Adjusting the SQL diagram to make the master-join filter explicit
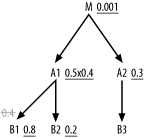
Now, it is clear that A1 offers a better filter than A2, so join to A1 first. After reaching A1, the database now has access to B1 or B2 as the next table to join. Comparing these to A2, you again find a better choice than A2. You join to B2 next, since you have already burned the benefit of the filtering join to B1. The complete optimum order, then, is (M, A1, B2, A2, B1, B3).
Next, consider the more complex problem represented by Figure 6-29, and try to solve it yourself before you read on.
Figure 6-29. Yet another query with a filtering master join
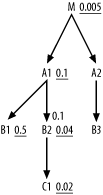
Considering first the best effective driving filter, adjust the filter ratio on A1 and the filter ratios below the filtering master join and find C2 offers an effective filter of 0.1 / 0.02=0.002. You could make the filter explicit on A1 as before with an is-not-null condition on the foreign key that points to B2, but this does not add sufficient selectivity to A1 to make it better than C1. The other alternatives are unadjusted filter ratios on the other nodes, but the best of these, 0.005 on M, is not as good as the effective driving filter on C2, so choose C2 for the driving table. From there, the filtering master join is no longer relevant, because the database will not join in that direction, and you find the full join order to be (C1, B2, A1, B1, M, A2, B3).
How would this change if the filter ratio on A1 were 0.01? By making the implied is-not-null condition on ForeignKeyToB2 explicit in the SQL, as before, you can make the multiple-condition filter selectivity 0.1 / 0.01=0.001, better than the effective filter ratio on C1, making A1 the best choice for driving table. With the join filter burned, you then choose the rest of the join order based on the simple filter ratios, finding the best order: (A1, B2, C1, B1, M, A2, B3) .
6.6.4 Close Filter Ratios
Occasionally, you find filter ratios that fall close enough in size to consider relaxing the heuristic rules to take advantage of secondary considerations in the join order. This might sound like it ought to be a common, important case, but it rarely matters, for several reasons:
When tables are big enough to matter, the application requires a lot of filtering to return a useful-sized (not too big) set of rows for a real-world application, especially if the query serves an online transaction. (End users do not find long lists of rows online or in reports to be useful.) This implies that the product of all filters is a small number when the query includes at least one large table.
Useful queries rarely have many filters, usually just one to three.
With few filters (but with the product of all filters being a small number), at least one filter must be quite small and selective. It is far easier to achieve sufficient selectivity reliably with one selective filter, potentially combined with a small number of at-best moderately selective filters, than with a group of almost equally selective filters.
With one filter that is much more selective than the rest, usually much more selective than the rest put together, the choice of driving table is easy.
Occasionally, you find near-ties on moderately selective filter ratios in choices of tables to join later in the execution plan. However, the order of later joins usually matters relatively little, as long as you start with the right table and use a robust plan that follows the join skeleton.
My own experience tuning queries confirms that it is rarely necessary to examine these secondary considerations. I have had to do this less than once per year of intensive tuning in my own experience.
Nevertheless, if you have read this far, you might want to know when to at least consider relaxing the simple rules, so here are some rule refinements that have rare usefulness in the case of near-ties:
Prefer to drive to smaller tables earlier. After you choose the driving table, the true benefit/cost ratio of joining to the next master table is (1-R)/C, where R is the filter ratio and C is the cost per row of reading that table through the primary key. Smaller tables are better cached and tend to have fewer index levels, making C smaller and making the benefit/cost ratio tend to be better for smaller tables.
|
Prefer to drive to tables that allow you to reach other tables with even better filter ratios sooner in the execution plan. The general objective is to discard as many rows as early in the execution plan as possible. Good (low) filter ratios achieve this well at each step, but you might need to look ahead a bit to nearby filters to see the full benefit of reaching a node sooner.
To compare nodes when choosing a driving table, compare the absolute values of the filter ratios directly; 0.01 and 0.001 are not close, but a factor of 10 apart, not a near-tie at all. Near-ties for the driving filter almost never happen, except when the application queries small tables either with no filters at all or with only moderately selective filters. In cases of queries that touch only small tables, you rarely need to tune the query; automated optimization easily produces a fast plan.
|
To compare nodes when choosing later joins, compare 1-R, where R is each node's filter ratio. In this context, filter ratios of 0.1 and 0.0001 are close. Even though these R values are a factor of 1,000 apart, the values of 1-R differ only by 10%, and the benefit/cost ratio (see the first rule in this list) would actually favor the less selective filter if that node were much smaller.
|
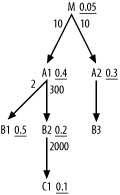
Figure 6-30 shows the first example with a near-tie that could lead to a break with the original simple heuristic rules. Try to work it out yourself before moving on.
Figure 6-30. A case to consider exceptions to the simple rules
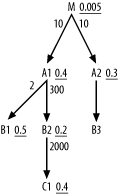
When choosing the driving node here, make no exception to the rules; M has far and away the best filter ratio from the perspective of choosing the driving table. The next choice is between A1 and A2, and you would normally prefer the lower filter ratio on A2. When you look at the detail join ratios from A1 to M and from A2 to M, you find that A1 and A2 are the same rowcount, so you have no reason on account of size to prefer either. However, when you look below these nearly tied nodes, note that A1 provides access to two nodes that look even better than A2. You should try to get to these earlier in the plan, so you would benefit moderately by choosing A1 first. After choosing A1 as the second table in the join order, the choice of third table is clear; B2 is both much smaller and better-filtered than A2.
|
The join order, so far, is (M, A1, B2). The choice of the next table is less obvious. C1 has a slightly worse filter ratio than A2 but is much smaller, by a factor of 300 x 2,000, so its cost per row is surely low enough to justify putting it ahead of A2 as well. The join order, so far, is now (M, A1, B2, C1), and the next eligible nodes are B1 and A2. The values for these nodes (1-R) are 0.5 and 0.7, respectively, and B1 is half the size of A2, making its expected cost per row at least a bit lower. If B1 were right on the edge of needing a new level in its primary-key index, A2 would likely have that extra index level and B1 might be the better choice next. However, since each level of an index increases the capacity by about a factor of 300, it is unlikely that the index is so close to the edge that this factor of 2 makes the difference. Otherwise, it is unlikely that the moderate size difference matters enough to override the simple rule based on filter ratio. Even if B1 is better than A2, by this point in the execution plan it will not make enough difference to matter; all four tables joined so far have efficiently filtered rows to this point. Now, the cost of these last table joins will be tiny, regardless of the choice, compared to the costs of the earlier joins. Therefore, choose the full join order (M, A1, B2, C1, A2, B1, B3).
Now, consider the problem in Figure 6-31, and try your hand again before you read on.
Figure 6-31. Another case to consider exceptions to the simple rules
This looks almost the same as the earlier case, but the filter on M is not so good, and the filters on the A1 branch are better, in total. The filter on M is twice as good as the filter on the next-best table, C1, but C1 has other benefits much smaller size, by a factor of 2,000 x 300 x 10, or 6,000,000, and it has proximity to other filters offering a net additional filter of 0.2 x 0.4 x 0.5=0.04. When you combine all the filters on the A1 branch, you find a net filter ratio of 0.04 x 0.1=0.004, more than a factor of 10 better than the filter ratio on M.
The whole point of choosing a driving table, usually choosing the one with the lowest filter ratio, is particularly to avoid reading more than a tiny fraction of the biggest table (usually the root table), since costs of reading rows on the biggest table tend to dominate query costs. However, here you find the database will reach just 8% as many rows in M if it begins on the A1 branch, rather than driving directly to the filter on M, so C1 is the better driving table by a comfortable margin. From there, just follow the normal rules, and find the full join order (C1, B2, A1, B1, M, A2, B3).
All these exceptions to the rules sound somewhat fuzzy and difficult, I know, but don't let that put you off or discourage you. I add the exceptions to be complete and to handle some rare special cases, but you will see these only once in a blue moon. You will almost always do just fine, far better than most, if you just apply the simple rules at the beginning of this chapter. In rare cases, you might find that the result is not quite as good as you would like, and then you can consider, if the stakes are really high, whether any of these exceptions might apply.
6.6.5 Cases to Consider Hash Joins
When a well-optimized query returns a modest number of rows, it is almost impossible for a hash join to yield a significant improvement over nested loops. However, occasionally, a large query can see significant benefit from hash joins, especially hash joins to small or well-filtered tables.
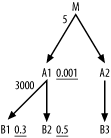
When you drive from the best-filtered table in a query, any join upward, from master table to detail table, inherits the selectivity of the driving filter and every other filter reached so far in the join order. For example, consider Figure 6-32. Following the usual rules, you drive from A1 with a filter ratio of 0.001 and reach two other filters of 0.3 and 0.5 on B1 and B2, respectively, on two downward joins. The next detail table join, to M, will normally reach that table, following the index on the foreign key that points to A1, on a fraction of rows equal to 0.00015 (0.001 x 0.3 x 0.5). If the detail table is large enough to matter and the query does not return an unreasonably large number of rows, this strategy almost guarantees that nested loops that follow foreign keys into detail tables win. Other join methods, such as a hash join that accesses the detail table independently, through its own filter, will read a larger fraction of that same table, since the best nested-loops alternative drives from the best filter ratio in the query.
Figure 6-32. Illustration of a query that favors hash joins
|
On the other hand, when you join downward to a master table, you might be joining to a much smaller table, and the cost of reaching the rows through the primary key might be larger than the cost of reading the table independently for a hash join. From the statistics in Figure 6-32, you would find 3,000 times as many rows in A1 as in B1. Even discarding 999 out of 1,000 rows from A1, the database would join to each row in B1 an average of three times. Assume that A1 has 3,000,000 rows and B1 has 1,000 rows. After winnowing A1 down to 3,000 rows, using the driving filter, the database would join to rows in the 1,000-row table B1 3,000 times. If the database drove into B1 with B1's own filter, it would need to read just 300 (0.3 x 1,000) rows, at roughly 1/10th the cost. Since the query reaches over 20% of the rows in B1, the database would find an even lower cost by simply performing a full table scan of B1 and filtering the result before doing the hash join. Therefore, while leaving the rest of the query cost unchanged, choosing a hash join to B1 would eliminate almost all the cost of the B1 table reads, compared to the standard robust plan that reads B1 through nested loops.
So, especially when you see large detail join ratios, hash joins to master tables can be fastest. How big is the improvement, though? In the example, the fractional improvement for this one table was high, over 90%, but the absolute improvement was quite modest, about 9,000 logical I/Os (6,000 in the two-level-deep key index and 3,000 on the table), which would take about 150 milliseconds. You would find no physical I/O at all to a table and index of this size. On the other hand, you would find the query reads about 2,250 (3,000 x 0.3 x 0.5 x 5) rows from the 15,000,000-row table M with 3,600 logical I/Os.
|
These 3,600 logical I/Os, especially the 2,250 to the table itself, will lead to hundreds of physical I/Os for such a large, hard-to-cache table. At 5-10 milliseconds per physical I/O, the reads to M could take seconds. This example is typical of cases in which hash joins perform best; these cases tend to deliver improvements only in logical I/Os to the smallest tables, and these improvements tend to be slight compared to the costs of the rest of the query.
A couple of rough formulae might help you choose the best join method:
- H=C x R
- L=C x D x F x N
The variables in these formulas are defined as follows:
- H
-
The number of logical I/Os necessary to read the master table independently, for purposes of a hash join.
- C
-
The rowcount of the master table.
- R
-
The master table's filter ratio. Assume the database reaches the table independently, through an index range scan on that filter.
- L
-
The number of logical I/Os to read the master table through nested loops on its primary key.
- D
-
The detail join ratio for the link that leads up from the master table, which normally tells you how much smaller it is than the detail table above it.
- F
-
The product of all filter ratios, including the driving filter ratio, reached before this join.
- N
-
The number of logical I/Os required per row read through the primary-key index.
Since primary keys up to 300 rows normally fit in the root block, N=2 (1 for the index root block and 1 for the table) for C up to 300. N=3 for C between roughly 300 and 90,000. N=4 for C between 90,000 and 27,000,000. Since you will normally drive from the best filter ratio, F<R, even if the plan picks up no additional filters after the driving-table filter.
H is less than L, favoring the hash join for logica







