G.1 Number Systems
Binary, Octal, and Hexadecimal Number System
Table G.1 lists the integers from 0 to 16, showing their equivalents in the binary (base 2), octal (base 8), and hexadecimal (base 16) number systems. The shaded cells in each column show the digits in each number system.
Decimal (base 10) | Binary (base 2) | Octal (base 8) | Hexadecimal (base 16) |
|---|---|---|---|
0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 |
2 | 10 | 2 | 2 |
3 | 11 | 3 | 3 |
4 | 100 | 4 | 4 |
5 | 101 | 5 | 5 |
6 | 110 | 6 | 6 |
7 | 111 | 7 | 7 |
8 | 1000 | 10 | 8 |
9 | 1001 | 11 | 9 |
10 | 1010 | 12 | a |
11 | 1011 | 13 | b |
12 | 1100 | 14 | c |
13 | 1101 | 15 | d |
14 | 1110 | 16 | e |
15 | 1111 | 17 | f |
16 | 10000 | 20 | 10 |
In addition to the decimal literals, Java also allows integer literals to be specified in octal and hexadecimal number systems, but not in the binary number system. Octal and hexadecimal numbers are specified with 0 and 0x prefix, respectively. The prefix 0X can also be used for hexadecimal numbers. Note that the leading 0 (zero) digit is not the uppercase letter O. The hexadecimal digits from a to f can also be specified with the corresponding uppercase forms (A to F). Negative integers (e.g., -90) can be specified by prefixing the minus sign (-) to the magnitude, regardless of number system (e.g., -0132 or -0X5A). The actual memory representation of the integer values is discussed in Section on page 598.
Converting Binary Numbers to Decimals
A binary number can be converted to its equivalent decimal value by computing the positional values of its digits. Each digit in the binary number contributes to the final decimal value by virtue of its position, starting with position 0 (units) for the right-most digit in the number. The positional value of each digit is given by
digit x base position
The number 1010012 corresponds to 4110 in the decimal number system:
1010012 | = 1x25 + 0x24 + 1x23 + 0x22 + 0x21 + 1x20 |
= 32 + 0 + 8 + 0 + 0 + 1 | |
= 4110 |
Converting Octal and Hexadecimal Numbers to Decimals
Similarly, octal (base 8) and hexadecimal (base 16) numbers can be converted to their decimal equivalents:
0132 = 1328 | = 1x82 + 3x81 + 2x80 | = 64 + 24 + 2 | = 9010 | Octal |
0x5a = 5a16 | = 5x162 + ax160 | = 80 + 10 | = 9010 | Hex |
The same technique can be used to convert a number from any base to its equivalent representation in the decimal number system.
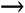 Decimal
Decimal






