Associations

Associations

Figure 4-1 shows a simple class model that would not surprise anyone who has worked with order processing. I'll describe each of the pieces and talk about how you would interpret them from the various perspectives.

I'll begin with the associations. Associations represent relationships between instances of classes (a person works for a company; a company has a number of offices).

From the conceptual perspective, associations represent conceptual relationships between classes. The diagram indicates that an Order has to come from a single Customer and that a Customer may make several Orders over time. Each of these Orders has several Order Lines, each of which refers to a single Product.

Each association has two association ends; each end is attached to one of the classes in the association. An end can be explicitly named with a label. This label is called a role name. (Association ends are often called roles.)

In Figure 4-1, the Order Line end of the association from Order is called line items. If there is no label, you name an end after the target classso, for instance, the Customer end of the association from Order would be called customer.

An association end also has multiplicity, which is an indication of how many objects may participate in the given relationship. In Figure 4-1, the * on the Order end of the association with Customer indicates that a Customer may have many Orders associated with it, whereas the 1 on the other end indicates that an Order comes from only one Customer.

In general, the multiplicity indicates lower and upper bounds for the participating objects. The * represents the range 0..infinity: A Customer need not have placed an Order, and there is no upper limit (in theory, at least!) to the number of Orders a Customer may place. The 1 stands for 1..1: An Order must have been placed by exactly one Customer.

The most common multiplicities in practice are 1, *, and 0..1 (you can have either none or one). For a more general multiplicity, you can have a single number (such as 11 for players on a cricket team), a range (such as 2..4 for players of a canasta game), or discrete combinations of numbers and ranges (such as 2, 4 for doors in a car before the onset of minivans).

Within the specification perspective, associations represent responsibilities.

Figure 4-1 implies that there are one or more methods associated with Customer that will tell me what orders a given Customer has made. Similarly, there are methods within Order that will let me know which Customer placed a given Order and what Line Items are on an Order.

If there are standard conventions for naming these query methods, I can probably infer from the diagram what these methods are called. For example, I may have a convention that says that single-valued relationships are implemented with a method that returns the related object, and that multivalued relationships are implemented with an iterator into a collection of the related objects.

Working with a naming convention like this in Java, for instance, I can infer the following interface for an Order class:

				
     class Order {
          public Customer getCustomer();
          public Set getOrderLines();
          ...

			

Obviously, programming conventions will vary from place to place and will not indicate every method, but they can be very useful in finding your way around.

An association also implies some responsibility for updating the relationship. There should be a way of relating the Order to the Customer. Again, the details are not shown; it could be that you specify the Customer in the constructor for the Order. Or, perhaps there is an addOrder method associated with Customer. You can make this more explicit by adding operations to the class box, as we will see later.

These responsibilities do not imply data structure, however. From a specification-level diagram, I can make no assumptions about the data structure of the classes. I cannot and should not be able to tell whether the Order class contains a pointer to Customer, or whether the Order class fulfills its responsibility by executing some selection code that asks each Customer whether it refers to a given Order. The diagram indicates only the interfacenothing more.

If this were an implementation model, we would now imply that there are pointers in both directions between the related classes. The diagram would now say that Order has a field that is a collection of pointers to Order Lines and also has a pointer to Customer. In Java, we could infer something like the following:

				
     class Order {
          private Customer _customer;
          private Set _orderLines;
     class Customer {
          private Set _orders;

			

In this case, most people assume that accessing operations are provided as well, but you can be sure only by looking at the operations on the class.

Now take a look at Figure 4-2. It is basically the same as Figure 4-1 except that I have added a couple of arrows on the association lines. These arrows indicatenavigability.

Figure 4-2. Class Diagram with Navigabilities

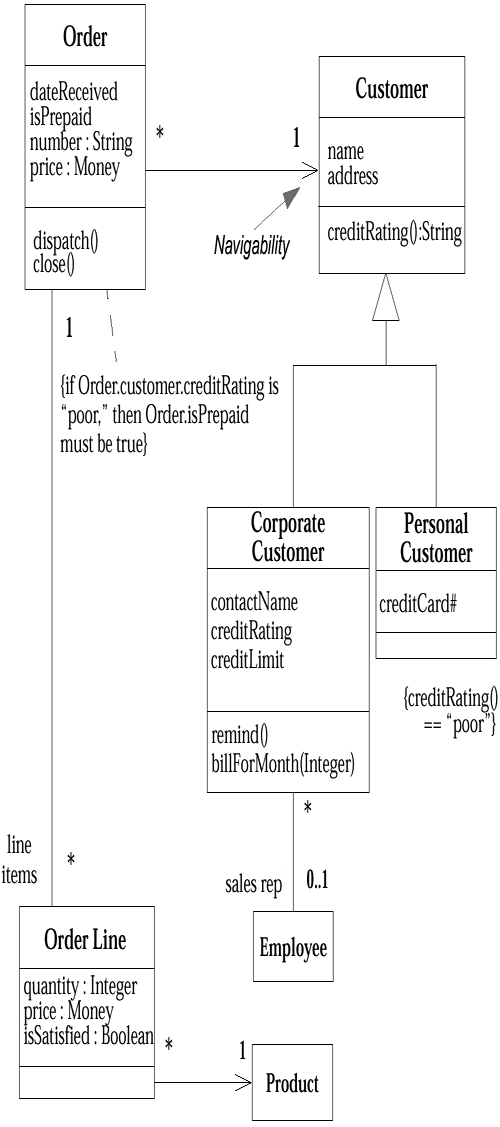
In a specification model, this would indicate that an Order has a responsibility to tell you which Customer it is for, but a Customer has no corresponding ability to tell you which Orders it has. Instead of symmetrical responsibilities, we now have responsibilities on only one end of the line. In an implementation diagram, this would indicate that Order contains a pointer to Customer, but Customer would not have a pointer to Order.

As you can see, navigability is an important part of implementation and specification diagrams. I don't think that navigability serves any useful purpose on conceptual diagrams, however.

You will often see a conceptual diagram that first appears with no navigabilities. Then the navigabilities are added as part of the shift to the specification and implementation perspectives. Note also that the navigabilities are likely to be different between specification and implementation.

If a navigability exists in only one direction, we call the association a unidirectional association. A bidirectional association contains navigabilities in both directions. The UML says that you treat associations without arrows to mean that either the navigability is unknown or the association is bidirectional. Your project should settle on one or the other meaning. I prefer it to mean "undecided" for specification and implementation models.

Bidirectional associations include an extra constraint, which is that the two navigations are inverses of each other. This is similar to the notion of inverse functions in math. In the context of Figure 4-2, this means that every Line Item associated with an Order must be associated with the original Order. Similarly, if you take an Order Line and look at the Line Items for its associated Order, you should see the original Order Line in the collection. This property holds true within all three perspectives.

There are several ways of naming associations. Traditional data modelers like to name an association using a verb phrase so that the relationship can be used in a sentence. Most object modelers prefer to use nouns to name the role of one or the other of the ends, since that corresponds better to responsibilities and operations.

Some people name every association. I choose to name an association only when doing so improves understanding. I've seen too many associations with names like "has" or "is related to." If there is no name on the end, I consider the name of the end to be the name of the attached class, as I indicated previously.

An association represents a permanent link between two objects. That is, the link exists during the whole lives of the objects, although the instances that are connected may change over time (or, in an optional association, be empty). So a parameter reference, or the creation of an object, does not imply an association; you model those with dependencies (see Chapters 6 and 7).