13.1 <algorithm>
The <algorithm> header declares the generic algorithm function templates for operating on iterators and other objects. Refer to Chapter 10 for more information about using and writing generic algorithms and about the iterators they use. See Chapter 8 for a discussion of iterator traits.
|
This section uses a number of abbreviations and conventions. First, each algorithm is described using plain English. Then, a more mathematical description of the algorithm, which tends to be harder to read, is given in a "Technical Notes" section.
The names of the template parameters tell you which category of iterator is expected. The iterator category is the minimal functionality needed, so you can, for example, use a random access iterator where at least a forward iterator is needed. (See Chapter 10 for more information on iterators and iterator categories.) To keep the syntax summaries short and readable, the iterator categories are abbreviated, as shown in Table 13-1.
|
Parameter name |
Iterator category |
|---|---|
|
BidiIter |
Bidirectional iterator |
|
FwdIter |
Forward iterator |
|
InIter |
Input iterator |
|
OutIter |
Output iterator |
|
RandIter |
Random access iterator |
Other template parameter names are chosen to be self-explanatory. For example, any name that ends in Predicate is a function that returns a Boolean result (which can be type bool or any other type that is convertible to bool) or a Boolean functional object (an object that has a function call operator that returns a Boolean result).
A number of algorithms require sorted ranges or otherwise use a comparison function to test the less-than relationship. The library overloads each algorithm: the first function uses operator<, and the second accepts a function pointer or function object to perform the comparison. The comparison function takes two arguments and returns a Boolean result. In the "Technical Notes" sections, the < relationship signifies operator< or the caller-supplied function, depending on the version of the algorithm you are using. If you overload operator< or provide your own comparison function, make sure it correctly implements a less-than relationship. In particular, a < a must be false for any a.
In this section, the following conventions are used:
Iterators are usually used in ranges that represent all the elements in the range or sequence. A range is written using standard mathematical notation: a square bracket denotes an inclusive endpoint of a range, and a parenthesis denotes an exclusive endpoint of a range. Thus, [x, y) is a range that starts at x, including x, and ends at y, excluding y. Chapter 10 also discusses this aspect of iterators.
Arithmetic expressions that involve iterators work as though each iterator were a random access iterator, even if the iterator is from a different category. For example, i - 1 for an input iterator is not allowed in C++ code, but in this section, it means the input iterator that points to one position before i.
The names used for input ranges are typically first and last, in which first is an iterator that points to first the element of the range, and last is an iterator that points to one past the end of the range. Thus, the range is written as [first, last).
An iterator that advances from first to last is typically called iter.
Output iterators are typically named result. Most algorithms specify only the start of the output range. It is your responsibility to ensure that the output range has room to accommodate the entire output. The behavior is undefined if the output range overflows.
In each "Technical Notes" section, conventional mathematical notation is used with some aspects of C++ notation, such as *, which dereferences an iterator. Also, a single equal sign (=) means assignment, and a double equal sign (==) means comparison for equality. The following conventions are used for names:
- i, j, k
-
Denote iterators, and *i, *j, and *k denote the values that the iterators point to.
- n, m
-
Denote integers.
- a, b, c
-
Denote values, which are usually of types that can be assigned to or from a dereferenced iterator (e.g., *i = a).
| adjacent_find function template | Searches for a pair of adjacent, equal items |
template<typename FwdIter> FwdIter adjacent_find(FwdIter first, FwdIter last); template<typename FwdIter, typename BinaryPredicate> FwdIter adjacent_find(FwdIter first, FwdIter last, BinaryPredicate pred); |
The adjacent_find function template looks for the first set of adjacent items in the range [first, last) that are equal (first version) or in which pred(*iter, (*iter+1)) is true (second version). Items are "adjacent" when their iterators differ by one position.
The return value is an iterator that points to the first of the adjacent items, or last if no matching items are found. See Figure 13-1 for an example.
Figure 13-1. Using adjacent_find to find two adjacent, equivalent items

Technical Notes
The adjacent_find function template returns i, in which i = first + n, and n is the smallest value such that *(first + n) == *(first + n + 1) and first + n + 1 < last, or, if there is no such n, i = last.
Complexity is linear: the standard is muddled, but any reasonable implementation calls the predicate (operator== or pred) exactly n + 1 times.
See Also
find function template, find_if function template
| binary_search function template | Searches using a binary search |
template<typename FwdIter, typename T> bool binary_search(FwdIter first, FwdIter last, const T& value); template<typename FwdIter, typename T, typename Compare> bool binary_search(FwdIter first, FwdIter last, const T& value, Compare comp); |
The binary_search function template uses a binary search to test whether value is in the range [first, last). It returns true upon success and false if the value is not found. The contents of the range must be sorted in ascending order.
The first version compares items using the < operator. The second version uses comp(X, Y) to test whether X < Y.
Technical Notes
Precondition: !(*(i + 1) < *i) for all i in [first, last - 1).
The binary_search function template returns true if there is an i in [first, last) such that !(*i < value) and !(value < *i). It returns false if there is no such i.
Complexity is logarithmic. The number of comparisons is at most log(last - first) + 2. Although the iterator can be a forward iterator, the best performance is obtained with a random access iterator. With a forward or bidirectional iterator, the iterator is advanced a linear number of times, even though the number of comparisons is logarithmic.
See Also
equal_range function template, find function template, find_if function template, lower_bound function template, upper_bound function template
| copy function template | Copies every item in a range |
template<typename InIter, typename OutIter>
OutIter copy(InIter first, InIter last, OutIter result);
|
The copy function template copies items from [first, last) to the output iterator starting at result. You must ensure that the output sequence has enough room for last - first items. The return value is the value of the result iterator after copying all the items, as shown in Figure 13-2.
Figure 13-2. Copying a range
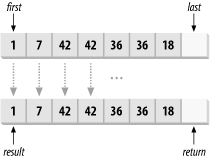
The result iterator cannot be in the source range [first, last), but other parts of the destination range can overlap with the source.
See Example 13-2 (under generate).
Technical Notes
The copy function template assigns *(result + n) = *(first + n) for all n in the range [0, last - first).
Complexity is linear: exactly last - first assignments are performed.
See Also
copy_backward function template, partial_sort_copy function template, replace_copy function template, remove_copy function template, reverse_copy function template, rotate_copy function template, unique_copy function template
| copy_backward function template | Copies a range, starting at the end |
template<typename BidiIter1, typename BidiIter2>
BidiIter2 copy_backward(BidiIter1 first, BidiIter1 last, BidiIter2 result);
|
The copy_backward function template does the same thing as copy, but it works backward, starting at the element before last and copying elements toward first. The result iterator must point to one past the end of the destination and is decremented before copying each element. The return value is an iterator that points to the first element of the destination, as shown in Figure 13-3.
Figure 13-3. Copying a range backward
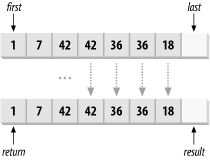
The result iterator cannot be in the source range [first, last), but other parts of the destination range can overlap with the source.
Technical Notes
The copy_backward function template assigns *(result - n) = *(last - n) for all n in the range [1, last - first].
Complexity is linear: exactly last - first assignments are performed.
See Also
copy function template, reverse_copy function template
| count function template | Counts the occurrences of a value |
template<typename InIter, typename T>
typename iterator_traits<InIter>::difference_type
count(InIter first, InIter last, const T& value);
|
The count function template returns the number of elements in the range [first, last) that are equal to value.
Technical Notes
Complexity is linear: exactly last - first comparisons are performed.
See Also
count_if function template, equal_range function template
| count_if function template | Counts the number of times a predicate returns true |
template<typename InIter, typename Predicate>
typename iterator_traits<InIter>::difference_type
count_if(InIter first, InIter last, Predicate pred);
|
The count_if function template returns the number of elements in the range [first, last) for which pred(*iter) returns true.
Technical Notes
Complexity is linear: pred is called exactly last - first times.
See Also
count function template, find_if function template
| equal function template | Tests whether ranges have same contents |
template<typename InIter1, typename InIter2> bool equal(InIter1 first1, InIter1 last1, InIter2 first2); template<typename InIter1, typename InIter2, typename BinaryPredicate> bool equal(InIter1 first1, InIter1 last1, InIter2 first2, BinaryPredicate pred); |
The equal function template returns true if two ranges contain the same elements in the same order. The first range is [first1, last1), and the second range has the same number of elements, starting at first2. The ranges can overlap.
The first form compares items using the == operator. The second form calls pred(*iter1, *iter2).
Technical Notes
The equal function template returns true if *(first1 + n) == *(first2 + n) for all n in the range [0, last1 - first1).
Complexity is linear: at most last1 - first1 comparisons are performed.
See Also
lexicographical_compare function template, mismatch function template, search function template
| equal_range function template | Finds all occurrences of a value in a sorted range using binary search |
template<typename FwdIter, typename T>
pair<FwdIter, FwdIter>
equal_range(FwdIter first, FwdIter last, const T& value);
template<typename FwdIter, typename T, typename Compare>
pair<FwdIter, FwdIter>
equal_range(FwdIter first, FwdIter last, const T& value, Compare comp);
|
The equal_range function template determines where value belongs in the sorted range [first, last). It returns a pair of iterators that specify the start and one past the end of the range of items that are equivalent to value, or both iterators in the pair point to where you can insert value and preserve the sorted nature of the range.
The first form compares values using the < operator. The second form calls comp(*iter, value).
Figure 13-4 shows how bounds are found with the value 36. The result of calling equal_range is pair(lb, ub). Note that for values in the range [19, 35], the upper and lower bound are both equal to lb, and for values in the range [37, 41], the upper and lower bound are both equal to ub.
Figure 13-4. Finding the limits of where the value 36 belongs in a sorted range
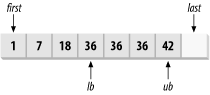
Technical Notes
Precondition: !(*(i + 1) < *i) for all i in [first, last - 1).
The equal_range function template returns the equivalent of calling the following, although the actual implementation might be different:
std::make_pair(std::lower_bound(first, last, value),
std::upper_bound(first, last, value))
or:
std::make_pair(std::lower_bound(first, last, value, comp),
std::upper_bound(first, last, value, comp))
Complexity is logarithmic. The number of comparisons is at most 2 x log(last - first) + 1. Although the iterator can be a forward iterator, the best performance is obtained with a random access iterator. With a forward or bidirectional iterator, the iterator is advanced a linear number of times, even though the number of comparisons is logarithmic.
See Also
binary_search function template, lower_bound function template, upper_bound function template, pair in <utility>
| fill function template | Fills a range with copies of a value |
template<typename FwdIter, typename T>
void fill(FwdIter first, FwdIter last, const T& value);
|
The fill function template fills the destination range [first, last) by assigning value to each item in the range.
Technical Notes
The fill function template assigns *i = value for all i in the range [first, last).
Complexity is linear: exactly last - first assignments are performed.
See Also
fill_n function template, generate function template
| fill_n function template | Fills a counted range with copies of a value |
template<typename OutIter, typename Size, typename T>
void fill_n(OutIter first, Size n, const T& value);
|
The fill_n function template assigns value to successive items in the destination range, starting at first and assigning exactly n items.
The Size template parameter must be convertible to an integral type.
Technical Notes
The fill_n function template assigns *(first + n) = value for all n in the range [0, n).
Complexity is linear: exactly n assignments are performed.
See Also
fill function template, generate_n function template
| find function template | Searches for a value using linear search |
template<typename InIter, typename T>
InIter find(InIter first, InIter last, const T& value);
|
The find function template returns an iterator that points to the first occurrence of value in [first, last). It returns last if value is not found. The == operator is used to compare items.
Technical Notes
The find function template returns i = first + n, in which n is the smallest value such that *(first + n) == value. If there is no such n, i = last.
Complexity is linear: at most last - first comparisons are performed.
See Also
find_end function template, find_first function template, find_if function template, search function template
| find_end function template | Searches for the last occurrence of a sequence |
template<typename FwdIter1, typename FwdIter2> FwdIter1 find_end(FwdIter1 first1, FwdIter1 last1, FwdIter2 first2, FwdIter2 last2); template<typename FwdIter1, typename FwdIter2, typename BinaryPredicate> FwdIter1 find_end(FwdIter1 first1, FwdIter1 last1, FwdIter2 first2, FwdIter2 last2, BinaryPredicate pred); |
The find_end function template finds the last (rightmost) subsequence [first2, last2) within the range [first1, last1), as illustrated in Figure 13-5. It returns an iterator, find_end in Figure 13-5, that points to the start of the matching subsequence or last1 if a match cannot be found.
The first form compares items with the == operator. The second form calls pred(*iter1, *iter2).
Figure 13-5. Finding a subsequence with find_end and search
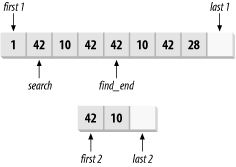
Technical Notes
Let length1 = last1 - first1 and length2 = last2 - first2.
The find_end function template returns first1 + n, in which n is the highest value in the range [0, length1 - length2) such that *(i + n + m) == (first2 + m) for all i in the range [first1, last1) and m in the range [0, length2). It returns last1 if no such n can be found.
Complexity: at most length1 x length2 comparisons are performed.
See Also
find function template, search function template
| find_first_of function template | Searches for any one of a sequence of values |
template<typename FwdIter1, typename FwdIter2> FwdIter1 find_first_of(FwdIter1 first1, FwdIter1 last1, FwdIter2 first2, FwdIter2 last2); template<typename FwdIter1, typename FwdIter2, typename BinaryPredicate> FwdIter1 find_first_of(FwdIter1 first1, FwdIter1 last1, FwdIter2 first2, FwdIter2 last2, BinaryPredicate pred); |
The find_first_of function template searches the range [first1, last1) for any one of the items in [first2, last2). If it finds a matching item, it returns an iterator that points to the matching item, in the range [first1, last1). It returns last1 if no matching item is found. Figure 13-6 shows an example.
Figure 13-6. Finding any one of a list of items
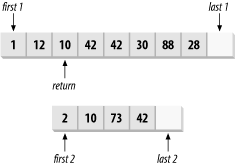
The first form compares items with the == operator. The second form calls pred(*iter1, *iter2).
Technical Notes
Let length1 = last1 - first1 and length2 = last2 - first2.
The find_first_of function template returns first1 + n where n is the smallest value in the range [0, length1) such that *(first1 + n) == (first2 + m) for some m in the range [0, length2). It returns last1 if no such n and m can be found.
Complexity: at most length1 x length2 comparisons are performed.
See Also
find function template
| find_if function template | Searches for when a predicate returns true |
template<typename InIter, typename Predicate>
InIter find_if(InIter first, InIter last, Predicate pred);
|
The find_if function template (similar to find) searches the range [first, last) for the first item for which pred(*iter) is true. It returns an iterator that points to the matching item. If no matching item is found, last is returned.
Technical Notes
The find_if function template returns i = first + n, in which n is the smallest value such that pred(*(first + n), value) is true. If there is no such n, i = last.
Complexity is linear: pred is called at most last - first times.
See Also
find function template
| for_each function template | Calls a function for each item in a range |
template<typename InIter, typename Func>
Function for_each(InIter first, InIter last, Func f);
|
The for_each function template calls f for each item in the range [first, last), passing the item as the sole argument to f. It returns f.
Example
Example 13-1 shows how the use for_each to test whether a sequence is sorted. The is_sorted object remembers the previous item in the sequence, which it compares with the current item. The overloaded bool operator returns true if the sequence is sorted so far or false if the sequence is out of order. The example takes advantage of the fact that for_each returns the f parameter as its result.
Example 13-1. Using for_each to test whether a list is sorted
#include <iostream>
#include <algorithm>
#include <list>
template<typename T>
class is_sorted
{
public:
is_sorted( ) : first_time(true), sorted(true) {}
void operator( )(const T& item) {
// for_each calls operator( ) for each item.
if (first_time)
first_time = false;
else if (item < prev_item)
sorted = false;
prev_item = item;
}
operator bool( ) { return sorted; }
private:
bool first_time;
bool sorted;
T prev_item;
};
int main( )
{
std::list<int> l;
l.push_back(10);
l.push_back(20);
...
if (std::for_each(l.begin( ), l.end( ), is_sorted<int>( )))
std::cout << "list is sorted" << '\n';
}
Technical Notes
Complexity is linear: f is called exactly last - first times.
See Also
copy function template, accumulate in <numeric>
| generate function template | Fills a range with values returned from a function |
template<typename FwdIter, typename Generator>
void generate(FwdIter first, FwdIter last, Generator gen);
|
The generate function template fills the sequence [first, last) by assigning the result of calling gen( ) repeatedly.
Example
Example 13-2 shows a simple way to fill a sequence with successive integers.
Example 13-2. Using generate to fill a vector with integers
#include <algorithm>
#include <iostream>
#include <iterator>
#include <vector>
// Generate a series of objects, starting with "start".
template <typename T>
class series {
public:
series(const T& start) : next(start) {}
T operator( )( ) { return next++; }
private:
T next;
};
int main( )
{
std::vector<int> v;
v.resize(10);
// Generate integers from 1 to 10.
std::generate(v.begin( ), v.end( ), series<int>(1));
// Print the integers, one per line.
std::copy(v.begin( ), v.end( ),
std::ostream_iterator<int>(std::cout, "\n"));
}
Technical Notes
Complexity is linear: gen is called exactly last - first times.
See Also
fill function template, generate_n function template
| generate_n function template | Fills a counted range with values returned from a function |
template<typename OutIter, typename Size, typename Generator>
void generate_n(OutIter first, Size n, Generator gen);
|
The generate_n function template calls gen( ) exactly n times, assigning the results to fill the sequence that starts at first. You must ensure that the sequence has room for at least n items. The Size type must be convertible to an integral type.
Example
Example 13-3 shows a simple way to print a sequence of integers.
Example 13-3. Using generate_n to print a series of integers
#include <algorithm>
#include <iostream>
#include <iterator>
// Use the same series template from Example 13-2.
int main( )
{
// Print integers from 1 to 10.
std::generate_n(std::ostream_iterator<int>(std::cout,"\n"),
10, series<int>(1));
}
Technical Notes
Complexity is linear: gen is called exactly n times.
See Also
fill_n function template , generate function template
| includes function template | Tests sorted ranges for subset |
template<typename InIter1, typename InIter2> bool includes(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2); template<typename InIter1, typename InIter2, typename Compare> bool includes(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2, Compare comp); |
The includes function template checks for a subset relationship, that is, it returns true if every element in the sorted sequence [first2, last2) is contained in the sorted sequence [first1, last1). It returns false otherwise.
Both sequences must be sorted. The first form uses the < operator to compare the elements. The second form calls comp(*iter1, *iter2).
Technical Notes
Precondition: !(*(i + 1) < *i) for all i in [first1, last1 - 1) and !(*(j + 1) < *j) for all j in [first2, last2 - 1).
The includes function template returns true if there is an i in [first1, last1) such that *(i + n) = *(first2 + n) for all n in [0, (last2 - first2)). It returns last1 if there is no such i.
Complexity is linear: at most, 2 x ((last1 - first1) + (last2 - first2)) - 1 comparisons are performed.
See Also
set_difference function template, set_intersection function template, set_symmetric_difference function template, set_union function template
| inplace_merge function template | Merges sorted, adjacent ranges in place |
template<typename BidiIter> void inplace_merge(BidiIter first, BidiIter middle, BidiIter last); template<typename BidiIter, typename Compare> void inplace_merge(BidiIter first, BidiIter middle, BidiIter last, Compare comp); |
The inplace_merge function template merges two sorted, consecutive ranges in place, creating a single sorted range. The two ranges are [first, middle) and [middle, last). The resulting range is [first, last).
The merge is stable, so elements retain their respective orders, with equivalent elements in the first range coming before elements in the second.
Both sequences must be sorted. The first form uses the < operator to compare elements. The second form calls comp(*iter1, *iter2).
Figure 13-7 shows how inplace_merge operates.
Figure 13-7. Merging two sorted ranges
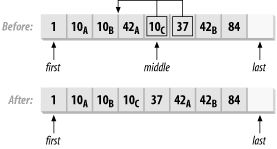
Technical Notes
Precondition: !(*(i + 1) < *i) for all i in [first, middle - 1) and !(*(j + 1) < *j) for all j in [middle, last - 1).
Postcondition: !(*(i + 1) < *i) for all i in [first, last - 1).
Complexity is usually linear with n + 1 comparisons, but if enough temporary memory is not available, the complexity might be n log n, in which n is last - first.
See Also
merge function template, sort function template
| iter_swap function template | Swaps values that iterators point to |
template<typename FwdIter1, typename FwdIter2>
void iter_swap(FwdIter1 a, FwdIter2 b);
|
The iter_swap function template swaps the values pointed to by a and b. You can think of its functionality as:
FdwIter1::value_type tmp = *b*; *b = *a; *a = tmp;
Technical Notes
Complexity is constant.
See Also
copy function template, swap function template, swap_ranges function template
| lexicographical_compare function template | Compares ranges for less-than |
template<typename InIter1, typename InIter2> bool lexicographical_compare(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2); template<typename InIter1, typename InIter2, typename Compare> bool lexicographical_compare(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2, Compare comp); |
The lexicographical_compare function template returns true if the sequence [first1, last1) is less than the sequence [first2, last2). If the sequences have the same length and contents, the return value is false. If the second sequence is a prefix of the first, true is returned. (The use of "lexicographical" emphasizes that the ranges are compared element-wise, like letters in words.)
The first form uses the < operator to compare elements. The second form calls comp(*iter1, *iter2).
Technical Notes
Let length1 = last1 - first1, length2 = last2 - first2, and minlength = min(length1, length2).
The lexicographical_compare function template returns true if either of the following conditions is true:
There is an n in [0, minlength) such that *(first1 + m) == *(first2 + m) for all m in [0, n - 1), and *(first1 + n) < *(first2 + n).
*(first1 + n) == *(first2 + n) for all n in [0, length2) and length2 < length1.
Complexity is linear: at most, minlength comparisons are performed.
Example
#include <algorithm>
#include <iostream>
#include <ostream>
int main( )
{
using namespace std;
int a[] = { 1, 10, 3, 42 };
int b[] = { 1, 10, 42, 3 };
int c[] = { 1, 10 };
cout << boolalpha;
cout << lexicographical_compare(a, a+4, b, b+4); // true
cout << lexicographical_compare(a, a+4, c, c+2); // false
cout << lexicographical_compare(a, a+4, a, a+4); // false
cout << lexicographical_compare(c, c+2, b, b+4); // true
}
See Also
equal function template
| lower_bound function template | Finds lower bound for a value's position in a sorted range using binary search |
template<typename FwdIter, typename T> FwdIter lower_bound(FwdIter first, FwdIter last, const T& value); template<typename FwdIter, typename T, typename Compare> FwdIter lower_bound(FwdIter first, FwdIter last, const T& value, Compare comp); |
The lower_bound function template determines where value belongs in the sorted range [first, last). The return value is an iterator that points to the first (leftmost) occurrence of value in the range, if value is present. Otherwise, the iterator points to the first position where you can insert value and preserve the sorted nature of the range.
The first form compares values using the < operator. The second form calls comp(*iter, value).
Figure 13-4 (under equal_range) shows how to find the bounds for the value 36. The lower_bound function returns lb as the lower bound of 36 in the given range. Note that lb is the lower bound for all values in the range [19, 36], and for values in the range [37, 41], the lower bound is equal to ub.
Technical Notes
Precondition: !(*(i + 1) < *i) for all i in [first, last - 1).
The lower_bound function template returns first + n, in which n is the highest value in [0, last - first) such that *(first + m) < value for all m in [0, n).
Complexity is logarithmic. The number of comparisons is at most log(last - first) + 1. Although the iterator can be a forward iterator, the best performance is obtained with a random access iterator. With a forward or bidirectional iterator, the iterator is advanced a linear number of times, even though the number of comparisons is logarithmic.
See Also
binary_search function template, equal_range function template, upper_bound function template
| make_heap function template | Reorders a range to convert it into a heap |
template<typename RandIter> void make_heap(RandIter first, RandIter last); template<typename RandIter, typename Compare> void make_heap(RandIter first, RandIter last, Compare comp); |
The make_heap function template reorders the elements in the range [first, last) to form a heap in place.
The first form compares values using the < operator. The second form calls comp(*iter, value).
Heap Data StructureA heap is a data structure that is ideally suited for implementing priority queues. C++ defines a range as a heap if two properties are satisfied:
The classic example of a heap is a binary tree, in which each node is greater than or equal to its children, but the relative order of the children is not specified. Thus, the root of the tree is the largest element in the entire tree. |
Technical Notes
Postcondition: [first, last) is a heap.
Complexity is linear: at most, 3 x (last - first) comparisons are performed.
See Also
pop_heap function template, push_heap function template, sort_heap function template, <queue>
| max function template | Returns the maximum of two values |
template<typename T> const T& max(const T& a, const T& b); template<typename T, typename Compare> const T& max(const T& a, const T& b, Compare comp); |
The max function template returns the larger of a and b. If neither is larger, it returns a.
The first form compares values using the < operator. The second form calls comp(a, b).
See Also
max_element function template, min function template
| max_element function template | Finds the largest element in a range |
template<typename FwdIter> FwdIter max_element(FwdIter first, FwdIter last); template<typename FwdIter, typename Compare> FwdIter max_element(FwdIter first, FwdIter last, Compare comp); |
The max_element function template returns an iterator that points to the largest element in the range [first, last). If there are multiple instances of the largest element, the iterator points to the first such instance.
The first form compares values using the < operator. The second form calls comp(*iter1, *iter2).
Technical Notes
The max_element function template returns first + n, in which n is the smallest value in [0, last - first) such that for all m in [0, last - first), *(first + n) < *(first + m) is false.
Complexity is linear: exactly max(last - first - 1, 0) comparisons are performed.
See Also
max function template, min_element function template
| merge function template | Merges sorted ranges |
template<typename InIter1, typename InIter2, typename OutIter> OutIter merge(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2, OutIter result); template<typename InIter1, typename InIter2, typename OutIter, typename Compare> OutIter merge(InIter1 first1, InIter1 last1, InIter2 first2, InIter2 last2, OutIter result, Compare comp); |
The merge function template merges the sorted ranges [first1, last1) and [first2, last2), copying the results into the sequence that starts with result. You must ensure that the destination has enough room for the entire merged sequence.
The return value is the end value of the destination iterator, that is, result + (last1 - first1) + (last2 - first2).
The destination range must not overlap either of the input ranges.
The merge is stable, so elements preserve their relative order. Equivalent elements are copied, so elements from the first range come before elements from the second range.
The first form compares values using the < operator. The second form calls comp(*iter1, *iter2).
Technical Notes
Let length1 = last1 - first1 and length2 = last2 - first2.
Precondition: !(*(i + 1) < *i) for all i in [first1, last1 - 1) and !(*(j + 1) < *j) for all j in [first2, last2 - 1).
Postcondition: !(*(i + 1) < *i) for all i in [result, result + length1 + length2 - 1).
Complexity is linear: at most, length1 + length2 - 1 comparisons are performed.
See Also
inplace_merge function template, sort function template
| min function template | Returns the minimum of two values |
template<typename T> const T& min(const T& a, const T& b); template<typename T, typename Compare> const T& min(const T& a, const T& b, Compare comp); |
The min function template returns the smaller of a and b. If neither is smaller, it returns a.
The first form compares values using the < operator. The second form calls comp(a, b).
See Also
max function template, min_element function template
| min_element function template | Finds the smallest value in a range |
template<typename FwdIter> FwdIter min_element(FwdIter first, FwdIter last); template<typename FwdIter, typename Compare> FwdIter min_element(FwdIter first, FwdIter last, Compare comp); |
The min_element function template returns an iterator that points to the smallest element in the range [first, last). If there are multiple instances of the smallest element, the iterator points to the first such instance.
The first form compares values using the < operator. The second form calls comp(*iter1, *iter2).
Technical Notes
The min_element function template returns first + n, in which n is the smallest value in [0, last - first) such that for all m in [0, last - first), *(first + m) < *(first + n) is false.
Complexity is linear: exactly max(last - first - 1, 0) comparisons are performed.
See Also
max_element function template, min function template
| mismatch function template | Finds first position where two ranges differ |
template<typename InIter1, typename InIter2>
pair<InIter1, InIter2>
mismatch(InIter1 first1, InIter1 last1, InIter2 first2);
template<typename InIter1, typename InIter2, typename BinaryPredicate>
pair<InIter1, InIter2>
mismatch(InIter1 first1, InIter1 last1, InIter2 first2,
BinaryPredicate pred);
|
The mismatch function template compares two sequences pairwise and returns a pair of iterators that identifies the first elements at which the sequences differ. The first sequence is [first1, last1), and the second sequence starts at first2 and has at least as many elements as the first sequence.
The return value is a pair of iterators; the first member of the pair points to an element of the first sequence, and second member of the pair points to an element of the second sequence. The two iterators have the same offset within their respective ranges. If the two sequences are equivalent, the pair returned is last1 and an iterator that points to the second sequence at the same offset (let's call it last2).
The first form compares items with the == operator. The second form calls pred(*iter1, *iter2).








