Set Theory
Set Theory
Set is a fundamental concept in all branches of mathematics and is also a very important concept for SQL because SQL queries operate with record sets. The idea of set is very intuitive: a collection of objects. The objects may be of the same type or of different types. In math terminology, set is a collection of well-defined objects; these objects are called the elements of the set. The elements (or members) of the set are said to belong to the set.
The listing of sets
Sets are usually denoted by capital letters and their elements by lowercase letters (or numbers). A set can contain anything and the elements of a set need not be the same kind of objects. In math notation a set can be defined by listing its elements between braces or by using set builder notation:
A = {1,2,5,8}
B = {x | x in N, 10 <= x <= 200}
The order of the elements does not matter:
{1,5,2,6} = {1,2,5,6} = {6,1,2,5}
Sets can contain other sets as elements
A = {1,3,{1,2},4,7}
assuming B = {1,2} and C = {7}, A = {1,3,B,4,C}.
The empty set is a set with no elements, denoted by {} or {Ø}.
In conventional set theory, repeated elements are ignored, or more specifically, repeated elements are treated as if they were a single element:
{a,a,c,b,c} = {a,b,c}
Sets need not be finite, and a typical example of an infinite set is the set of all integers:
Z = {...,–2,–1,0,1,2,...}
Another typical example is the set of natural numbers, which consists of all nonnegative integers:
N = {1,2,3,...}
Yet another example is the set of whole numbers:
W = {0,1,2,...}.
Sometimes a set is difficult or impossible to list; for example, the set of all natural numbers from 10 to 200. In such cases we can define the set by stating the properties of its elements:
A = {x | x in N, 10 <= x <= 200}
This notation is read as A is the set of all x such that x is a natural number (N) and x lies between 10 and 200 inclusive.
Subsets
We say that a set P is a subset of set Q if every element of P is also an element of Q. This does not exclude the possibility that P = Q.
For example, if:
A = {1,2,3,4,5,6}
B = {1,3,7}
C = {2,4,6}
then C is a subset of A, but B is not a subset of A because it contains element 7 that is not a member of set A.
| Note |
Related to the concept of subsets is that of the superset. A is a superset of C, which means that A contains C. |
Set equality
Two sets, A and B, are equal if A is a subset of B and B is a subset of A. In other words, A = B if every element of A is also in B and every element of B is also in A.
Operations on sets
Operations on sets include union, intersection, complement, difference, and Cartesian product.
UNION
The union of two sets A and B is the set containing all elements in A or B or both. It is written as A U B. The union of n sets, A1, A2, ..., An is the set of all objects which belong to at least one of the sets:
A = {2,5}
B = {1,9}
A U B = {1,2,5,9}.
Figure L-1 illustrates the concept.
 Figure L-1: Set union
Figure L-1: Set union
| Note |
In SQL, the UNION operator works exactly as described here. If the resulting set contains duplicates, they are excluded. For example, {1,2,5} U {1,5,9} = {1,2,5,9}. To preserve duplicates SQL uses another operator, UNION ALL that is not a part of the classical set theory. If you denote UNION ALL with UA, then {1,2,5} UA {1,5,9} = {1,1,2,5,5,9}. |
INTERSECTION
The intersection of two sets A and B is the set of all common elements that are found in both A and B. It is written as A ^ B. The intersection of n sets, A1, A2, ..., An is the set of all objects that belong to every one of the sets:
A = {a,b,d}
B = {d,e,f}
A ^ B = {d}
Intersection is shown on Figure L-2.
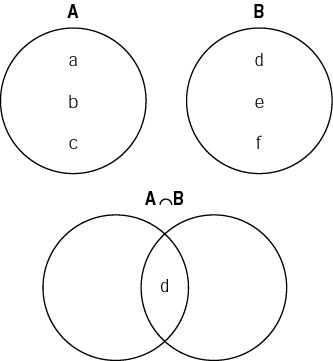
Figure L-2: Set intersection
COMPLEMENT
The complement (or absolute complement) of a set A is the set NOT(A) or A' consisting of all elements not in A. This definition requires the existence of a Universal set U:
A = {a,b,c}
U = {a,b,c,...,z}
A' = {d,e,f,...,z}
| Note |
In the SQL99 standards (and all the "big three" databases) the complement is denoted by the NOT operator. |
DIFFERENCE
The difference of sets A and B is defined as the set A – B consisting of all elements of A that are not also in B. The difference of A and B is not the same as the difference of B and A. The definition of set difference does not imply that A and B have anything in common, nor does it say anything about their relative sizes:
A = {1,3,5,7,8}
B = {3,4,6,8,10}
A – B = {1,5,7}
B – A = {4,6,10}.
Set difference is illustrated in Figure L-3.

Figure L-3: Set difference
| Note |
The DIFFERENCE set operator is represented by EXCEPT in SQL99 and DB2 (MINUS in Oracle). MS SQL Server does not have any operator for set difference; the result can be simulated using NOT EXISTS. See Chapter 8 for more information. |
CARTESIAN PRODUCT
The Cartesian product of two sets A and B denoted by A × B (also called the product set or the product of A and B) is a set of ordered pairs where the first component is a member of the first set and the second component is a member of the second set:
A = {1,2,3}
B = {7,8}
A × B = {(1,7), (1,8), (2,7), (2,8), (3,7), (3,8)}
Figure L-4 represents the Cartesian product.

Figure L-4: Cartesian product
| Note |
Cartesian product is also known as a CROSS JOIN in SQL99 and MS SQL Server. |
Multiple operations
For multiple unions and intersections, brackets can be used to clarify the order of operations, e.g., ( A ^ B ) U C.
Set cardinality
Cardinality is the term describing the number of elements in a set. It is denoted by |A|:
A = {1,3,5}
|A| = 3
B = {a,b,f,r,t,y}
|B| = 6
| Note |
For the empty set, |{}| = 0. |
Identities of Set algebra
Set algebra identities are listed in Table L-14.
|
Name |
Identity |
|---|---|
|
Idempotent laws |
A U A = A
|
|
Associative laws |
A U (B U C) = (A U B) U C
|
|
Commutative laws |
A U B = B U AA ^ B = B ^ A |
|
Distributive laws |
A U (B ^ C) = (A U B) ^ (A U C) |
|
Identity laws |
A U {} = A
|
|
Complement laws |
A U A' = U |
|
DeMorgan's laws |
(A ^ B)' = A' U B' |








