3.1 Global Alignment: Needleman-Wunsch

The global alignment algorithm described here is called the Needleman-Wunsch algorithm. We will explain it in a way that seems natural to biologists, that is, it tells the end of the story first, and then fills in the details. (This is why biologists make terrible comedians; they always tell the punch line first.) We will align the words COELANCANTH and PELICAN using a simple scoring scheme: +1 for letters that match, -1 for mismatches, and -1 for gaps. The alignment will eventually look like one of the following, which are equivalent given our scoring scheme:

COELACANTH      COELACANTH
P-ELICAN--      -PELICAN--

Note that every letter of each sequence is aligned to a letter or a gap. In local alignments, discussed later, this isn't the case.

The alignment takes place in a two-dimensional matrix in which each cell corresponds to a pairing of one letter from each sequence. To get an intuitive understanding of the alignment algorithm, look at Figure 3-1, which shows where the maximum scoring alignment lies in the matrix. The alignment starts at the upper left and follows a mostly diagonal path down and to the right. When two letters are aligned, the path follows a diagonal trajectory. There are several places in which the letters from COELACANTH are paired to gap characters. In this case, the graph is followed horizontally. Although not shown here, the path may be also be followed vertically when the letters from PELICAN are paired with gap characters. Gap characters can never be paired to each other. Note that the first row and column are blank. The reason for this will become clear shortly.

Figure 3-1. Example of an alignment matrix

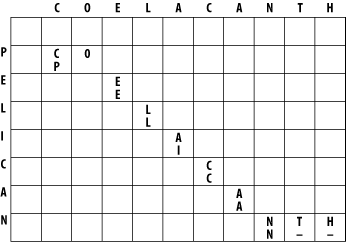
In reality, you don't store letters in the matrix as shown in Figure 3-1. Each cell of the matrix actually contains two values: a score and a pointer. The score is derived from the scoring scheme. Here, this means +1 or -1, but when aligning biological sequences, the values come from a scoring matrix (a topic of the next chapter). The pointer is a directional indicator (an arrow) that points up, left, or diagonally up and left. The pointer navigates the matrix, and its use will become clearer later in the chapter. Now, let's look at the algorithm in detail. There are three major phases: initialization, fill, and trace-back.

3.1.1 Initialization

In the initialization phase, you assign values for the first row and column (Figure 3-2). The next stage of the algorithm depends on this. The score of each cell is set to the gap score multiplied by the distance from the origin. Gaps may be present at the beginning of either sequence, and their cost is the same as anywhere else. The arrows all point back to the origin, which ensures that alignments go all the way back to the origin (a requirement for global alignment).

Figure 3-2. Initialization of the alignment matrix

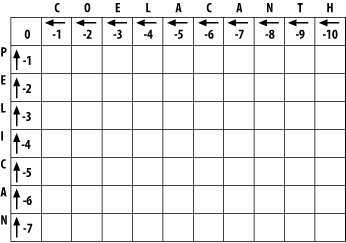
3.1.2 Fill

In the fill phase (also called induction), the entire matrix is filled with scores and pointers using a simple operation that requires the scores from the diagonal, vertical, and horizontal neighboring cells. You will compute three scores: a match score, a vertical gap score, and a horizontal gap score. The match score is the sum of the diagonal cell score and the score for a match (+1 or -1). The horizontal gap score is the sum of the cell to the left and the gap score (-1), and the vertical gap score is computed analogously. Once you've computed these scores, assign the maximum value to the cell and point the arrow in the direction of the maximum score. Continue this operation until the entire matrix is filled, and each cell contains the score and pointer to the best possible alignment at that point.

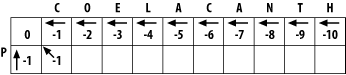
If you look at the initialized matrix, you'll find that there's only one cell where you can compute the maximum score because there's only one cell with the required 3 neighbors. Now you can see why you needed to leave one extra column and row and why you needed the initialization phase. Without them, you wouldn't be able to start the fill. Ignoring the rest of the table, compute this cell (the one that matches C to P).

The match score is the sum of the preceding diagonal cell (score = 0) and the score for aligning C to P (-1). The total match score is -1. The horizontal gap score is the sum of the score to the left (-1) and the gap score (-1). The horizontal gap score is therefore -2. The same is true for the vertical gap score. Your maximum score is therefore the diagonal score (-1), and the pointer is set to the diagonal (Figure 3-3). Now that this first cell is computed, you can compute the cell to the right or the cell below. Calculate one more cell, the right neighbor (the one that aligns O and P).

Figure 3-3. Beginning to fill the alignment matrix

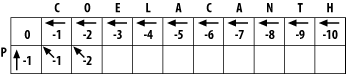
The match score is the sum of the preceding diagonal cell (-1) and the mismatch score (-1), which equals -2. The horizontal gap score is the score of the cell to the left (-1) and the gap penalty (-1), which is also -2. The vertical gap score is the cell above (-2) and the gap penalty (-1), which totals -3. The maximum score is -2, but this can come from the diagonal or from the left. This is where you must make a consistent, arbitrary choice?for example, always choose the diagonal over a gap.

The matrix up to this point is shown in Figure 3-4. It may seem rather trivial, but the maximum global alignment between CO and P can be calculated. It has a score of -2 and has either of the following equivalent forms:

CO    CO
-P    P-

Figure 3-4. Second cell filled in the alignment matrix

Using the same maximizing procedure for each cell, you can fill the entire matrix. At the end of the fill, the matrix appears as in Figure 3-5.

Figure 3-5. Filled alignment matrix

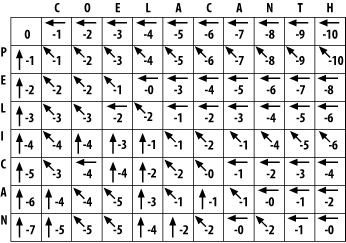
3.1.3 Trace-Back

The trace-back lets you recover the alignment from the matrix. Like the other parts of this algorithm, it's pretty simple. Start at the bottom-right corner and follow the arrows until you get to the beginning. To produce the alignment, at each cell, write out the corresponding letters or a hyphen for the gap symbol. Since you're following it from the end to the start, the alignment will be backward, and you just reverse it. The final alignment looks like this:

COELACANTH
-PELICAN- 

Example 3-1 shows a Perl script.

Example 3-1. Trace-back with Needleman-Wunsch algorithm

# Needleman-Wunsch  Algorithm 

# usage statement
die "usage: $0 <sequence 1> <sequence 2>\n" unless @ARGV == 2;

# get sequences from command line
my ($seq1, $seq2) = @ARGV;

# scoring scheme
my $MATCH    =  1; # +1 for letters that match
my $MISMATCH = -1; # -1 for letters that mismatch
my $GAP      = -1; # -1 for any gap

# initialization
my @matrix;
$matrix[0][0]{score}   = 0;
$matrix[0][0]{pointer} = "none";
for(my $j = 1; $j <= length($seq1); $j++) {
    $matrix[0][$j]{score}   = $GAP * $j;
    $matrix[0][$j]{pointer} = "left";
}
for (my $i = 1; $i <= length($seq2); $i++) {
    $matrix[$i][0]{score}   = $GAP * $i;
    $matrix[$i][0]{pointer} = "up";
}

# fill
for(my $i = 1; $i <= length($seq2); $i++) {
    for(my $j = 1; $j <= length($seq1); $j++) {
        my ($diagonal_score, $left_score, $up_score);

        # calculate match score
        my $letter1 = substr($seq1, $j-1, 1);
        my $letter2 = substr($seq2, $i-1, 1);                            
        if ($letter1 eq $letter2) {
            $diagonal_score = $matrix[$i-1][$j-1]{score} + $MATCH;
        }
        else {
            $diagonal_score = $matrix[$i-1][$j-1]{score} + $MISMATCH;
        }

        # calculate gap scores
        $up_score   = $matrix[$i-1][$j]{score} + $GAP;
        $left_score = $matrix[$i][$j-1]{score} + $GAP;

        # choose best score
        if ($diagonal_score >= $up_score) {
            if ($diagonal_score >= $left_score) {
                $matrix[$i][$j]{score}   = $diagonal_score;
                $matrix[$i][$j]{pointer} = "diagonal";
            }
        else {
                $matrix[$i][$j]{score}   = $left_score;
                $matrix[$i][$j]{pointer} = "left";
            }
        } else {
            if ($up_score >= $left_score) {
                $matrix[$i][$j]{score}   = $up_score;
                $matrix[$i][$j]{pointer} = "up";
            }
            else {
                $matrix[$i][$j]{score}   = $left_score;
                $matrix[$i][$j]{pointer} = "left";
            }
        }
    }
}

# trace-back

my $align1 = "";
my $align2 = "";

# start at last cell of matrix
my $j = length($seq1);
my $i = length($seq2);

while (1) {
    last if $matrix[$i][$j]{pointer} eq "none"; # ends at first cell of matrix

    if ($matrix[$i][$j]{pointer} eq "diagonal") {
        $align1 .= substr($seq1, $j-1, 1);
        $align2 .= substr($seq2, $i-1, 1);
        $i--;
        $j--;
    }
    elsif ($matrix[$i][$j]{pointer} eq "left") {
        $align1 .= substr($seq1, $j-1, 1);
        $align2 .= "-";
        $j--;
    }
    elsif ($matrix[$i][$j]{pointer} eq "up") {
        $align1 .= "-";
        $align2 .= substr($seq2, $i-1, 1);
        $i--;
    }    
}

$align1 = reverse $align1;
$align2 = reverse $align2;
print "$align1\n";
print "$align2\n";