7.1 Basic BLAST Statistics
Primary BLAST literature doesn't focus on the arithmetic involved in calculating an Expect. Understandably, the papers discuss the theoretical underpinnings of Karlin-Altschul statistics, leaving BLAST users without the kinds of examples found in a text book. This chapter provides this missing information.
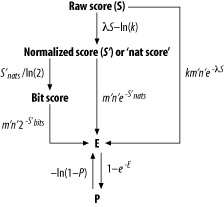
Figure 7-1 summarizes the basic operations involved in converting the raw score of a high-scoring pair into an Expect, or P-value. The following discussion explains how to perform each calculation and any accessory operations required to derive an Expect.
Figure 7-1. The essential calculations involved in converting an HSP's raw score into a probability
Calculating Karlin-Altschul statistics isn't easily done with a pencil, paper, and calculator. Applying Karlin-Altschul statistics to an HSP and avoiding a migraine requires code. We use simple Perl subroutines to take the grind out of the calculations and help clarify the equations. Hopefully these subroutines will also provide a basis for further investigations of your own BLAST results. If you'd like to add these subroutines to your codebase, you can download them from this book's web site; the module name is BlastStats.pm.
Example 7-1 shows a sample HSP from a BLASTP search. Use this alignment as a reference to check your calculations.[1] For our present purposes, the details of the search aren't important, but the values given in the header and footer of the report are. The header and footer are omitted from the search that generated this alignment.
[1] If you plan to perform the calculations described in this chapter and have searched the NCBI web site (http://www.ncbi.nlm.nih.gov/BLAST), make sure you don't select the composition-based statistics in the Advanced Options checkbox because the values of the composition-based lambdas aren't given in the report. Currently, it's selected by default for BLASTP, and you unselect it by clicking on it.
Example 7-1. A sample HSP from a BLASTP search
>CT12121 translation from_gene[CG3603 CG3603 FBgn0029648]
seq_release:2 mol_weight=18568
cds_boundaries:(X:2,699,992..2,700,667[+]) aa_length:176
transcript_info:[CT12121 seq_release:2] gene_info:[gene
symbol:CG3603 FBgn0029648
gene_boundaries:(X:2,699,935..2,700,670[+]) (GO:0016614
"oxidoreductase, acting on CH-OH group of donors")]
Length = 176
Score = 70.9 bits (172), Expect = 8e-13
Identities = 49/170 (28%), Positives = 85/170 (49%), Gaps = 6/170 (3%)
Query: 50 IAGEVAVVTGAGHGLGRAISLELAKKGCHIAVVDINVSGAEDTVKQIQDIYKVRAKAYKA 109
+AG+VA+VTGAG G+GRA LA+ G + VD N+ A++TV Q++ R+ A +
Sbjct: 6 LAGKVALVTGAGSGIGRATCRLLARDGAKVIAVDRNLKAAQETV---QELGSERSAALEV 62
Query: 110 NVTNYDDLVELNSKVVEEMGPV-TVLVNNAGVMMHRNMFNPDPADVQLMINVNLTSHFWT 168
+V++ + ++ +++ T++VN+AG+ + D + VNL F
Sbjct: 63 DVSSAQSVQFSVAEALKKFQQAPTIVVNSAGITRDGYLLKMPERDYDDVYGVNLKGTFLV 122
Query: 169 KLVFLPKM--KELRKGFIVTISSLAGVFPLPYSATYTTTKSGALAHMRTL 216
+ M ++L G IV +SS+ A Y TK+G ++ L
Sbjct: 123 TQAYAKAMIEQKLENGTIVNLSSIVAKMNNVGQANYAATKAGVISFTERL 172
|
Parameter |
Value |
|---|---|
|
l |
0.267 nats (gapped) |
|
k |
0.0410 nats (gapped) |
|
H |
0.140 nats/aligned residue |
|
m |
321 (length of the query sequence) |
|
n |
9418064 (number of letters in the database searched) |
|
Effective HSP length |
99 |
|
Number of sequences in database |
17878 |
7.1.1 Actual Versus Effective Lengths
The Karlin-Altschul equation
![]() is probably the most
recognized equation in bioinformatics. It states that the number of
alignments expected by chance (E) during a
sequence database search is a function of the size of the search space
(m*n), the normalized score
(lS), and a minor constant
(k). (For more information about the
Karlin-Altschul equation and its associated parameters, see Chapter 4). The first step toward understanding how to
use the Karlin-Altschul equation is to understand what values for
m and n BLAST uses when
calculating an Expect. Many users assume that the m
and n in the equation refer to the
length of the query and subject sequences; this isn't the case. In
practice, you use the effective lengths rather
than actual lengths of the query and database when calculating the
Expect of an
HSP.
is probably the most
recognized equation in bioinformatics. It states that the number of
alignments expected by chance (E) during a
sequence database search is a function of the size of the search space
(m*n), the normalized score
(lS), and a minor constant
(k). (For more information about the
Karlin-Altschul equation and its associated parameters, see Chapter 4). The first step toward understanding how to
use the Karlin-Altschul equation is to understand what values for
m and n BLAST uses when
calculating an Expect. Many users assume that the m
and n in the equation refer to the
length of the query and subject sequences; this isn't the case. In
practice, you use the effective lengths rather
than actual lengths of the query and database when calculating the
Expect of an
HSP.
The terms used in the BLAST literature to denote the actualand effective lengths of the query, subject, and database can be confusing. Sometimes m and n denote actual lengths, and sometimes they denote the effective lengths. To avoid confusion, this chapter uses m and n to denote actual lengths and m´ and n´ to denote effective lengths.
The effective length of the query, m´, is its actual length minus the expected HSP length. The effective length of the database, n´, is the sum of the effective length of every sequence within it. In other words, if the sequence database used in a BLAST search contains only a single sequence, the actual length of that database, n, is the length of that sequence; the effective length, n´, of that database is the effective length of the single sequence it contains. If the database contains two sequences, its actual length is the sum of the lengths of those two sequences; the effective length of that database is the sum of those two sequences' effective lengths.
Calculating m´ and n´ requires knowing the expected HSP length, which is the length of an HSP that has an Expect of 1. You can find this value in the NCBI-BLAST report footer (where it's called, confusingly, effective HSP length). You can also calculate it, as you'll learn later in this chapter. For now, though, use the value from Table 7-1. Here are two Perl functions used to calculate m´ and n´:
sub effectiveLengthSeq {
my $m = shift; # actual length sequence
my $expected_HSP_length = shift;
my $k = shift; # gapped k
my $m_prime = $m - $expected_HSP_length;
if ($m_prime < 1/$k){
return 1/$k;
}
else {
return $m_prime;
}
}
sub effectiveLengthDb {
my $n = shift; # actual length
my $expected_HSP_length = shift;
my $num_seqs_in_db = shift;
my $k = shift; # gapped k
my $n_prime = $n - ($num_seqs_in_db*$expected_HSP_length);
if ($n_prime < 1/$k){
return 1/$k;
}
else {
return $n_prime;
}
}
Notice that no effective length of the query or the database can ever be less than 1/k. Setting an effective length to 1/k basically amounts to ignoring a short sequence for statistical purposes; in cases when both m and n are less than 1/k, BLAST searches are ill-advised. For more information about effective lengths and short sequences, see Chapter 4.
Using these functions with the information provided in Table 7-1 gives a value of 222 and 7648142 for m´ and n´, respectively.
7.1.2 The Raw Score and Bit Score
BLAST reports two scores: the raw score and a normalized score called abit score. The raw score, S, is the sum of the alignment's pair-wise scores using a specific scoring matrix (see Chapter 4 for more information). When deriving the bit score for an HSP, first convert its raw score to a nat score using the following equation:
![]()
Because BLAST reports l in nats (or more precisely, nats per unit raw score) rather than bits, you must divide the nat score, S´, by ln(2) to convert it to a bit score. As you become a more critical user and interpreter of BLAST reports, you may find yourself converting nats to bits and raw scores to bit scores regularly. The following two Perl subroutines convert bits to nats, and vice versa:
sub nToB {
my $n = shift;
return $n/log(2); # converts nats to bits
}
sub bToN {
my $n = shift;
return $n*log(2); # converts bits to nats
}
Try using l and k tocalculate the bit score for the alignment shown in Figure 7-1. If you use the following Perl function and the values of kand l given in Table 7-1, you get a bit score of 70.9 for a raw score of 172.
sub rawScoreToBitScore {
my $raw_score = shift;
my $k = shift;
my $l = shift; #lambda in nats
# S'bits = (lnatsS - ln (k))/ln(2)
return nToB($l*$raw_score - log($k));
}
7.1.3 The Expect of an HSP
Now
calculate the Expect for the HSP shown in Figure 7-1, recalling that
![]() . Again, a simple Perl function is useful:
. Again, a simple Perl function is useful:
sub rawScoreToExpect {
my $raw_score = shift;
my $k = shift;
my $l = shift; # lambda in nats
my $m = shift; # effective length of query
my $n = shift; # effective length of database
# E = km'n'e-lS
return $k*$m*$n*exp(-1*$l*$raw_score);
}
Using this function, the values of kand l, given in Table 7-1, combined with the values m´ (222) and n´ (7648142) that you calculated in your discussion of effective lengths, gives an Expect of 8e-13 for the alignment shown in Figure 7-1.
You can
also calculate the Expect of an alignment with a normalized score,
S´ (Figure 7-1).
The Karlin-Altschul equation
![]() is formulated for the raw
score, S, not the normalized score
S´. To calculate an Expect using a
normalized score S´ whose units are nats,
use the equation E = m'n'e-S'. Note that k doesn't appear in this equation; it has already been accounted for when deriving the normalized (nat) score (e.g.,
is formulated for the raw
score, S, not the normalized score
S´. To calculate an Expect using a
normalized score S´ whose units are nats,
use the equation E = m'n'e-S'. Note that k doesn't appear in this equation; it has already been accounted for when deriving the normalized (nat) score (e.g., ![]() ).
).
To calculate the Expect of an HSP from its bit score (Figure 7-1) use the Perl function shown next. The formula is similar to that used to calculate an Expect from a nat score. However, the base of the exponent is 2 rather than e because you're using bits rather than nats.
sub bitScoreToExpect {
my $bit_score = shift;
my $m = shift; # effective length query
my $n = shift; # effective length of database
# reformulated for bits
# E = m'n'2-bit_score
return $m*$n*2**(-1*$bit_score);
}
7.1.4 The WU-BLAST P-Value
Another important difference between
WU-BLAST and NCBI-BLAST is that WU-BLAST reports a P-value as well as
an Expect for an alignment. The two functions shown below will
convert between these two related measures of statistical
significance. Because P is equal to
1-e-E, P![]() E if either value is less than
0.001.
E if either value is less than
0.001.
sub EtoP {
my $e = shift;
# P = 1 - e-E
return 1-exp(-1*$e);
}
sub PtoE {
my $p = shift;
# E = -ln(1 - P)
return -1*log(1-$p);
}
Some of the calculations discussed in
this chapter don't apply to sum statistics. The sum
score for a set of alignments isn't merely the sum
of the raw scores for a set of HSPs. Likewise, the familiar
![]() equation isn't used when calculating the Expect of a sum score. Thus, the rawScoreToBitScore, rawScoreToExpect, and bitScoreToExpect functions must be modified for sum statistics.
equation isn't used when calculating the Expect of a sum score. Thus, the rawScoreToBitScore, rawScoreToExpect, and bitScoreToExpect functions must be modified for sum statistics.
7.1.5 Sum Statistics
Now that you've
learned how BLAST calculates the Expect of an individual HSP,
let's examine how BLAST assigns an Expect to a group
of HSPs. Unlike the Smith-Waterman algorithm, which finds the single
maximum scoring alignment, BLAST finds multiple high-scoring pairs.
As a result, aligning two sequences often results in multiple HSPs.
In some cases, BLAST groups several HSPs in a hit,[2] recalculates,
and reports their aggregate statistical significance in place of each
HSP's individual Expect. The ubiquitous
Karlin-Altschul equation
![]() isn't used to calculate the aggregate statistical significance of a group of HSPs; instead, a related measure is used that employs a sum score..
isn't used to calculate the aggregate statistical significance of a group of HSPs; instead, a related measure is used that employs a sum score..
[2] Here hit means one or more HSPs. You'll encounter the word "hit" frequently in the BLAST literature and when using BLAST.
Many BLAST users are surprised to learn the BLAST employs not one, but two measures of statistical significance. This misconception is understandable, as little in a BLAST report alerts the casual user to this fact. In the default BLAST format, the only indication that sum statistics were applied to a set of HSPs is the presence of the Expect(n) (in an NCBI BLAST report) and the Sum P(n) (in a WU-BLAST report). Figure 7-2 provides an overview of the procedure used by NCBI-BLAST to derive an Expect(n), and the following section discusses each calculation in detail.
Figure 7-2. The essential calculations involved in deriving the aggregate Expect for a group of HSPs
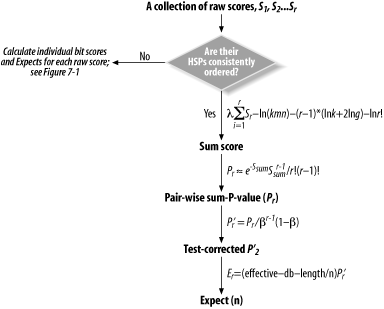
7.1.6 An Expect(n) Means That Sum Statistics Were Applied
Unless you know what to look for, you probably won't notice that the output in Example 7-2 contains two HSPs that were grouped for statistical purposes. The reported Expect(2) for these two alignments is the Expect for their combined or sum score rather than their reported bit scores. As such, it doesn't refer to the actual statistical significance of either alignment's reported bit score.
Example 7-2. Two BLASTX HSPs to which sum statistics were applied
Score = 71.2 bits (173), Expect(2) = 1e-15
Identities = 31/59 (52%), Positives = 44/59 (74%)
Frame = -1
Query: 24837 WLDFLYYCSYVKLTITIIKYVPQALMNYRRKSTSGWSIGNILLDFTGGTLSMLQMILNA 24661
WL + + +++ +T +KY+PQA MN+ RKST GWSIGNILLDFTGG + LQM++ +
Sbjct: 148 WLWLISIFNSIQVFMTCVKYIPQAKMNFTRKSTVGWSIGNILLDFTGGLANYLQMVIQS 206
Score = 38.5 bits (88), Expect(2) = 1e-15
Identities = 15/34 (44%), Positives = 21/34 (61%)
Frame = -3
Query: 24595 DDWVSIFGDPTKFGLGLFSVLFDVFFMLQHYVFY 24494
+ W + +G+ K L L S+ FD+ FM QHYV Y
Sbjct: 210 NSWKNFYGNMGKTLLSLISIFFDILFMFQHYVLY 243
The reported Expect(2) for both alignments is identical, yet their reported raw scores are 173 and 88, respectively. Obviously, the reported Expect for these two alignments can't have been calculated using these raw scores. When BLAST applies sum statistics to a set of HSPs, it uses their sum score to calculate their combined Expect. Unfortunately, this score isn't available anywhere in the report. (For more information about sum scores, see Chapter 4). The sum score, however, can be calculated with the various parameters listed in Table 7-2. These values are taken from the same search as the BLASTX hit shown in Example 7-2. Normally, these values are located in the header and footer of a BLAST report.
|
Parameter |
Value |
|---|---|
|
l |
0.267 nats (gapped) |
|
k |
0.0410 nats (gapped) |
|
H |
0.140 nats/aligned residue |
|
m |
40206 (length of the query sequence) |
|
n |
270 (length of the subject sequence) |
|
Gap decay constant |
0.1 |
|
Effective _db_length |
78368169 |
|
Effective HSP length |
144 |
7.1.7 Sum Statistics Are Pair-Wise in Their Focus
Pair-wise is a term to consider when thinking
about sum statistics. Previous discussions of BLAST statistics
involved formulations that are most intuitive in the context of
database searches; for example, the n in the
equation
![]() refers to the size of the database. Yes, a database may sometimes consist of a single sequence, but in most cases it won't. The published formulations for sum statistics, on the other hand, are pair-wise in their focus; only after all the pair-wise scores and significance values are calculated are adjustments made for database size. In the following discussion, for example, n refers to the actual length of the subject sequence of the alignment, no matter how many sequences make up the database.
refers to the size of the database. Yes, a database may sometimes consist of a single sequence, but in most cases it won't. The published formulations for sum statistics, on the other hand, are pair-wise in their focus; only after all the pair-wise scores and significance values are calculated are adjustments made for database size. In the following discussion, for example, n refers to the actual length of the subject sequence of the alignment, no matter how many sequences make up the database.
7.1.8 The Sum Score
While neither WU-BLAST nor NCBI-BLAST reports the sum score for a group of HSPs anywhere in its output, this invisible number is the basic currency of sum statistics; thus, you should understand how it's calculated. Whether or not sum statistics are applied to a group of HSPs depends on the details of the alignments themselves. If the HSPs are ordered consistently with respect to the subject and query begin and end coordinates, BLAST calculates a sum score. If not, it reports the raw score and individual Expect for each HSP in the BLAST Hit. The following Perl function calculates the (pair-wise-ordered) sum score for a collection of r HSPs. (For more information about sum scores see Chapter 4.)
sub sumScore {
my $raw_scores = shift; # raw scores are in an array reference
my $k = shift;
my $l = shift;
my $m = shift; # effective length of query sequence
my $n = shift; # effective length of sbjct sequence
my $g = shift; # gap_size;for NCBI-BLAST this value is 50
my $r = @{$raw_scores};
die "do not take sum for a single score!\n"
if $r == 1;
my $total_raw_score = 0;
foreach my $individual_raw_score (@{$raw_scores}){
$total_raw_score += $individual_raw_score;
}
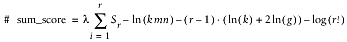 my $n_score = $l*$total_raw_score;
return
$n_score - log($k*$m*$n)-($r -1)*(log($k)+2*log($g))-log(fac($r));
}
my $n_score = $l*$total_raw_score;
return
$n_score - log($k*$m*$n)-($r -1)*(log($k)+2*log($g))-log(fac($r));
}
7.1.9 Effective Length of a BLASTX Query
To calculate a sum score, you need to calculate the effective length of the query sequence. Recall, however, that for BLASTX, the query is a nucleotide sequence, and yet a partial translation of that sequence is being aligned. What, then, is its effective length of m´, for purposes of sum score calculations? BLASTX considers the effective length of the nucleotide query sequence, m´, to be equal to its translated actual length (m/3) minus the expected HSP length. The following Perl function calculates the effective length of a BLASTX query:
sub effectiveLengthOfBlastxQuery {
my $m = shift; # actual nucleotide length of the query
my $exp = shift; # expected HSP length.
# m' = m/3-expected_HSP_length
return $m/3 - $exp;
}
Recall that calculating a sum score also requires you to calculate the effective length, n´, of the subject sequence. To do so, use the Perl function, effectiveLengthSeq, given earlier in the chapter, because it also applies to the subject sequence for purposes of calculating a sum score.
7.1.10 Calculating a Sum Score
If you look at Example 7-2, you'll see that these two BLASTX HSPs comprise an ordered set. In other words, these two alignments suggest that the query sequence contains a minus strand gene, at least two exons of which are homologous to the subject sequence. Because these two alignments comprise a consistently ordered set, you will calculate their pair-wise ordered sum score. Using the Perl function sumScore that's in Section 7.1.8, the sum score for these two HSPs is about 53 nats, or 77 bits.
7.1.11 Calculating the Pair-Wise Sum P-Value
The sum score (77 bits) for these two HSPs isn't much more than that of the first HSP's individual bit score (71.2). Why, then, is the resulting Expect (2) for these two HSPs so low: Expect (2) = 1e-15, when the first HSP with only a slightly lower bit score has a much less significant individual Expect of 3.7e-10?
The reason for the discrepancy is that the familiar Karlin-Altschul
equation
![]() isn't used when calculating the Expect of a sum score. Sum statistics uses a very different formula. In fact, an Expect isn't calculated, but rather a pair-wise sum P-value. A Perl function for calculating this value is shown next:
isn't used when calculating the Expect of a sum score. Sum statistics uses a very different formula. In fact, an Expect isn't calculated, but rather a pair-wise sum P-value. A Perl function for calculating this value is shown next:
sub pairwiseSumP {
my $sumS = shift; # the sum score
my $r = shift; # number of HSPs being combined
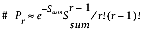 return (exp(-1*$sumS)*$sumS**fac($r-1))/(fac($r)*fac($r -1));
}
sub fac {
my $r = shift;
my $fac;
for (my $i = $r; $i > 0; $i--){
$fac = defined($fac) ? $fac*$i: $i;
}
$fac = 1 unless defined($fac);
return $fac;
}
return (exp(-1*$sumS)*$sumS**fac($r-1))/(fac($r)*fac($r -1));
}
sub fac {
my $r = shift;
my $fac;
for (my $i = $r; $i > 0; $i--){
$fac = defined($fac) ? $fac*$i: $i;
}
$fac = 1 unless defined($fac);
return $fac;
}
Using this function, the pair-wise sum P of a sum score of 53 nats is about 2e-22. That's a lot less than the reported Expect(2) of 1e-15. The discrepancy occurs because 2e-22 isn't the Expect(2), but the pair-wise P-value for these two alignments. You must perform two additional calculations using thepair-wise P-value to derive the Expect(n). First, adjust the pair-wise sum P-value for additional significance tests performed when identifying combinations of alignments whose sum P is more significant than any one of its member's individual significance. Second, convert the adjusted P-value into an Expect(n) by correcting for database size.
7.1.12 Correcting for Multiple Tests
BLAST will group a set of HSPs only if the Expect(n) of the group is less than the Expect of any individual member, and if that group is an optimal partition such that no other grouping might result is a lower Expect(n). Identifying these optimal groups is done internally by BLAST and requires testing many potential groups for statistical significance. You must make a correction for these tests. BLAST uses a test-correction function that takes the number of HSPs in the group?the "n" of the Expect(n), rather than the actual number of comparisons made. A function for performing this correction on the pair-wise sum P-value is shown next. In the function, r is simply the number of HSPs being grouped. Because you're dealing with an Expect(2) in Example 7-2, r = 2 (again, see Chapter 4 for more information).
sub rTestsCorrectedP {
my $r = shift;
my $sum_p = shift;
my $beta = shift; # gap decay constant
# P'r = Pr/br-1(1-b)
return $sumP/($beta**($r-1)*(1-$beta));
}
b in the function above is the gap
decay constant which, by default, is 0.1 for NCBI-BLASTX. Applying
this function to the pair-wise sum P-value gives a test-corrected
value of 2.2e-21. This value isn't very
different from the original, as when r = 2, so
![]() is equal to 1/11. Notice,
however, that for values of r > 5, this correction becomes much less trivial.
is equal to 1/11. Notice,
however, that for values of r > 5, this correction becomes much less trivial.
7.1.13 Correcting for Database Size
Converting the (test-corrected) pair-wise sum P-value to a database-size corrected Expect is the final step in calculating an Expect(n). How best to do this isn't an axiomatic issue, but a practical one. Chapter 4 discusses some of the issues surrounding database size correction in more detail. NCBI-BLASTX applies a size correction that assumes the number of HSPs are proportional to the length of the subject sequence.
sub dbSizeCorrectedExpect {
my $sumP = shift; # test corrected sumP
my $effective_db_length_db = shift;
my $sbjct_seq_length = shift; # actual length
# = (effective_db_length_db/n)P
return ($effective_db_length_db/$sbjct_seq_length)*$sumP;
}
Using this function, the test-corrected, pair-wise sum P-value of 2.2e-21 gives an Expect(2) of 7e-16, a fairly close match to the reported value (in Example 7-2) of 1e-15. The difference between the two values can be attributed to rounding and floating-point error.
7.1.14 Frame- and Size-Corrected Expects
BLASTX translates all six frames of the query and uses these translations to search the protein database. At first, you might think that correcting for six frames would entail multiplying the final database-size-corrected Expect by six, but that isn't the case. Neither version of BLASTX applies such a correction. In fact, WU-BLASTX posts a notice in its header stating that it doesn't apply the correction (illustrated in Example 7-3). Like NCBI-BLAST, WU-BLAST searches all six frames by default, but assumes that only one frame was searched when calculating Expects. The reason why is that BLAST statistics assume open reading frames don't overlap. Accordingly, BLASTX statistics assume that the query contains only a single ORF whose frame may change from HSP to HSP.
Example 7-3. The header from a WU-BLASTX report
BLASTX 2.0MP-WashU [09-Nov-2000] [linux-i686 19:13:41 11-Nov-2000]
Copyright (C) 1996-2000 Washington University, Saint Louis, Missouri USA.
All Rights Reserved.
Reference: Gish, W. (1996-2000) http://blast.wustl.edu
Gish, Warren and David J. States (1993). Identification of protein coding
regions by database similarity search. Nat. Genet. 3:266-72.
Notice: statistical significance is estimated under the assumption that the
equivalent of one entire reading frame in the query sequence codes for protein
and that significant alignments will involve only coding reading frames.
Query= 3R 3R.3 [18846615 18886821] flank:20000 length:40206
(40,206 letters)
Translating both strands of query sequence in all 6 reading frames
Database: rscu.fsa
386,401 sequences; 134,009,913 total letters.
Searching....10....20....30....40....50....60....70....80....90....100% done
So far in this chapter, we've just walked through most basic operations of Karlin-Altschul statistics to provide you with the knowledge necessary to calculate bit scores, effective lengths, and Expects. We've explained that BLAST uses one statistical measure to calculate the Expect of an HSP and another to calculate the aggregate Expect of a group of HSPs. Hopefully, you've gained a better understanding of how all of these operations of fit into the larger picture of Karlin-Altschul statistics.
You have also seen that it's possible to use Karlin-Altschul statistics to recover statistical measures that are calculated by BLAST internally, but not included in the report?principally, sum scores and the individual Expect for an HSP for which an Expect(n) has been reported. Learning to calculate these values is the first step toward becoming a power user of BLAST statistics. The remaining sections of this chapter will show you how to use what you've learned to deal with critical questions about BLAST results.







