3.2 Local Alignment: Smith-Waterman
The local alignment algorithm we describe here, the Smith-Waterman algorithm, is a very simple modification of Needleman-Wunsch. There are only three changes:
The edges of the matrix are initialized to 0 instead of increasing gap penalties.
The maximum score is never less than 0, and no pointer is recorded unless the score is greater than 0.
The trace-back starts from the highest score in the matrix (rather than at the end of the matrix) and ends at a score of 0 (rather than the start of the matrix).
These simple changes have a profound effect on the behavior of algorithm. Using the same words and scoring scheme as you did in global alignment, look at the filled matrix in Figure 3-6.
Figure 3-6. Filled Smith-Waterman alignment matrix
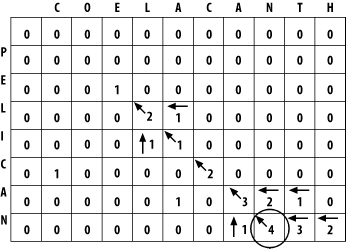
As you can see, there are a lot of zeroes. That's because there are a lot of places where you can't get a positive score. Also note that one cell is circled. This is the cell with the maximum score in the matrix. There may be more than one place in the matrix with the same maximum score, and in this case, some kind of arbitrary decision must be made. Start your trace-back from the maximum score and follow it to a score of zero, creating your alignment as you step backward, just as you did with global alignment. At the end, you have an alignment with a score of 4 that looks like this:
ELACAN ELICAN
Example 3-2 shows the Perl code.
Example 3-2. Local alignment with the Smith-Waterman algorithm
# Smith-Waterman Algorithm
# usage statement
die "usage: $0 <sequence 1> <sequence 2>\n" unless @ARGV == 2;
# get sequences from command line
my ($seq1, $seq2) = @ARGV;
# scoring scheme
my $MATCH = 1; # +1 for letters that match
my $MISMATCH = -1; # -1 for letters that mismatch
my $GAP = -1; # -1 for any gap
# initialization
my @matrix;
$matrix[0][0]{score} = 0;
$matrix[0][0]{pointer} = "none";
for(my $j = 1; $j <= length($seq1); $j++) {
$matrix[0][$j]{score} = 0;
$matrix[0][$j]{pointer} = "none";
}
for (my $i = 1; $i <= length($seq2); $i++) {
$matrix[$i][0]{score} = 0;
$matrix[$i][0]{pointer} = "none";
}
# fill
my $max_i = 0;
my $max_j = 0;
my $max_score = 0;
for(my $i = 1; $i <= length($seq2); $i++) {
for(my $j = 1; $j <= length($seq1); $j++) {
my ($diagonal_score, $left_score, $up_score);
# calculate match score
my $letter1 = substr($seq1, $j-1, 1);
my $letter2 = substr($seq2, $i-1, 1);
if ($letter1 eq $letter2) {
$diagonal_score = $matrix[$i-1][$j-1]{score} + $MATCH;
}
else {
$diagonal_score = $matrix[$i-1][$j-1]{score} + $MISMATCH;
}
# calculate gap scores
$up_score = $matrix[$i-1][$j]{score} + $GAP;
$left_score = $matrix[$i][$j-1]{score} + $GAP;
if ($diagonal_score <= 0 and $up_score <= 0 and $left_score <= 0) {
$matrix[$i][$j]{score} = 0;
$matrix[$i][$j]{pointer} = "none";
next; # terminate this iteration of the loop
}
# choose best score
if ($diagonal_score >= $up_score) {
if ($diagonal_score >= $left_score) {
$matrix[$i][$j]{score} = $diagonal_score;
$matrix[$i][$j]{pointer} = "diagonal";
}
else {
$matrix[$i][$j]{score} = $left_score;
$matrix[$i][$j]{pointer} = "left";
}
} else {
if ($up_score >= $left_score) {
$matrix[$i][$j]{score} = $up_score;
$matrix[$i][$j]{pointer} = "up";
}
else {
$matrix[$i][$j]{score} = $left_score;
$matrix[$i][$j]{pointer} = "left";
}
}
# set maximum score
if ($matrix[$i][$j]{score} > $max_score) {
$max_i = $i;
$max_j = $j;
$max_score = $matrix[$i][$j]{score};
}
}
}
# trace-back
my $align1 = "";
my $align2 = "";
my $j = $max_j;
my $i = $max_i;
while (1) {
last if $matrix[$i][$j]{pointer} eq "none";
if ($matrix[$i][$j]{pointer} eq "diagonal") {
$align1 .= substr($seq1, $j-1, 1);
$align2 .= substr($seq2, $i-1, 1);
$i--; $j--;
}
elsif ($matrix[$i][$j]{pointer} eq "left") {
$align1 .= substr($seq1, $j-1, 1);
$align2 .= "-";
$j--;
}
elsif ($matrix[$i][$j]{pointer} eq "up") {
$align1 .= "-";
$align2 .= substr($seq2, $i-1, 1);
$i--;
}
}
$align1 = reverse $align1;
$align2 = reverse $align2;
print "$align1\n";
print "$align2\n";







