Computing the Temporal Keys
Earlier we described how the temporal keys are generated from the master keys, but we were not specific about how this is accomplished. Obviously the derivation must be done in a very specific way; any ambiguity might result in two different vendors' products deriving keys that don't match and hence failing to work together. We casually mentioned earlier that the key information needed to be expanded?getting more bits that we started with. For example, although the PMK is 256 bits, it has to be expanded into 512 bits before being divided up into the four temporal keys.
This section explains how the key generation and computation is done. In practice, both generation and expansion occur during the same process. Key expansion seems counterintuitive because it implies that additional bits are generated from "thin air." However, the object is not to increase the size of the base key (in other words, the key entropy), but to derive several keys, all of which appear unrelated to an outside observer. For example, in the case of the four pairwise temporal keys, if an attacker knows one of the four temporal keys, it should be impossible to derive any of the others. It doesn't matter how many bits you expand the master key into, the strength against brute force attacks remains the same.
The approach to key expansion is to use a pseudorandom number generator (PRNG) and keep generating random bytes until you have enough for your key expansion. The starting condition or seed of the PRNG is based on the known information such as your master keys. Diagrammatically, this relationship is shown in Figure 10.9, which is really an expanded version of Figure 10.2, the key computation block. An important point is that, given the same seed, the PRNG always produces the same "random" output stream so two independent devices can generate the same set of keys by starting with the same seed value.
Figure 10.9. Temporal Key Computation
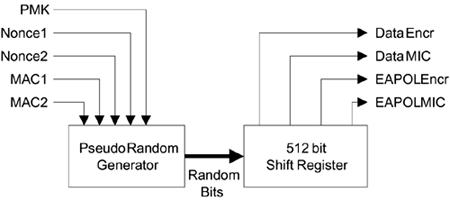
The PRNG function is used in several places in RSN and WPA. For example, it was used to generate the starting nonce; it is used to expand the pairwise keys and also to generate the GTK. This would create a potential problem if the same PRNG were to be used in each of these different cases. If you want a random stream of data for two different purposes in a security system, you must be absolutely sure that they will not both use an identical pseudorandom stream. On the other hand, we would like to use a single PRNG function for implementation efficiency, so what is needed is a PRNG that is guaranteed to provide a different stream for different uses even when the seed information appears the same.
To achieve this, RSN and WPA define a set of pseudorandom functions, each incorporating a different text string into the input. There are different functions, each designed to produce a certain number of bits. These are referred to as PRF-n, where n is the number of bits required. The defined choices are:
PRF-128
PRF-256
PRF-384
PRF-512
Each function takes three parameters and produces the desired number of random bits. The three parameters are:
A secret key (K)
A text string specific to the application (e.g., nonce generation versus pairwise key expansion)
Some data specific to each case, such as nonces or MAC addresses
The notation used for these functions is: PRF-n(K, A, B). So, for example, when we specify that the starting value for the nonce is:
Starting nonce = PRF-256(Random Number, "Init Counter", MAC || Time)
it means that the PRF-256 function is invoked with:
K | = | Random number |
A | = | The text string "Init Counter" |
B | = | A sequence of bytes formed by the MAC address followed by a number representing time |
In a similar way, the computation of the pairwise temporal keys is written:
PRF-512(PMK, "Pairwise key expansion", MAC1||MAC2||Nonce1||Nonce2)
Here MAC1 and MAC2 are the MAC addresses of the two devices where MAC1 is the smaller (numerically) and MAC2 is the larger of the two addresses. Similarly, Nonce1 is the smallest value between ANonce and SNonce, while Nonce2 is the largest of the two values.
The group temporal keys are derived as follows:
PRF-256(GMK, "Group key expansion", MAC||GNonce)
Here, MAC is the MAC address of the authenticator, that is, the access point for infrastructure networks.
We see how all the various keys can be derived by using PRF-n, so how is the PRF-n implemented? Obviously, this has to be carefully specified if we hope to have interoperability.
All the variants of PRF are implemented using the same algorithm based on HMAC-SHA-1.[8] We have seen HMAC-MD5 before; it was used to produce the MIC for EAPOL-Key messages. But we are not generating a MIC here; we want a random number generator. Like HMAC-MD5, HMAC-SHA-1 is also a hashing algorithm that can be used to generate MIC values. It is approved by the US National Institute for Science and Technology (NIST; www.nist.gov), which publishes the details of the algorithm. The method of computation is different from MD5, but the effect is the same. They both take in a stream of data and produce a message digest of fixed length. HMAC-MD5 produces 16 bytes and HMAC-SHA-1 produces 20 bytes. The message digest is quite unpredictable (except by using the algorithm) and tells you nothing about the contents of the message that was "digested." Even if you changed one single bit in input message, an entirely new digest would be produced with no apparent connection to the previous value. There's a clue to how we can make a hashing algorithm into a pseudorandom number generator.
[8] SHA stands for secure hash algorithm.
We take a message and hash it using HMAC-SHA-1 to get a 160-bit (20-byte) result. Now change one bit in the input message and produce another 160 bits. We already know that this 160 bits appears unrelated to the first one, so if we put them together, we get 320 bits of apparently random data. By repeating this process, we can generate a pseudorandom stream of almost any number of bits. This is how HMAC-SHA-1 is used to implement the PRF-n functions. Here are the details:
Start with the function PRF-n (K, A, B) where n can be 128, 256, 384, or 512.
Initialize a single byte counter variable i to 0.
Create a block of data by concatenating the following:
A (the application-specific text)
0 (a single 0 byte)
B (the special data)
i (the counter, a single byte value)
This is written: A|0|B|i
Compute the hash of this block of data using key K:
r = HMAC-SHA-1(K, A|0|B|i)
Store the value of r for later in a register called R.
Now repeat this calculation as many times as needed to generate the needed number of random bits (because 160 are generated each time, you may get more than you need, whereupon the extra bits are discarded). Before each iteration, increment the counter i by one and after each iteration appending the result bits r to the register R.
After the required number of iterations, you have your random stream of bytes.







