AES Overview
AES is a block cipher. Using mathematical and logical operations, the method combines a key and a 128-bit block of data (unencrypted) to produce a block of different data (encrypted). For all practical purposes, it is impossible perform this transform if you don't know the key. AES is reversible (that is, you can convert back to the original data using decryption), which is useful, but not essential to all security protocols. The encrypted and unencrypted blocks are exactly the same size. The conversion of a single block of 128 bits of data is all that AES does?but it does it quite efficiently and is extremely secure. It is very unlikely that any fundamental weakness will be discovered in future.
AES is based on the Rijndael algorithm, invented by Joan Daeman and Vincent Rijmen. This algorithm is very well documented, including the algorithm and implementation details (Daeman and Rijmen, 2000, 2001). The overview in this book provides a flavor of the method and does not attempt to provide any mathematical justification, although it is necessary to look at some of the quirky arithmetic involved.
The Rijndael algorithm allows for a selection of block sizes and key sizes. The choices are 128, 192, or 256 bits for each. When NIST adopted Rijndael for AES, it specified only one block size, 128 bits, but retained the choice of three key lengths. IEEE 802.11i goes one step further and restricts both the key size and the block length to 128 bits. This simplifies implementation and relieves the users of having to make yet another choice during installation.
Modes of Operation
You can use AES to encrypt and decrypt a single fixed length block of data. However, in practice real messages do not occur as fixed-length blocks. Wi-Fi LAN data, for example, is transmitted in frames of various different lengths, typically between 512 to 12,000 bits in each frame. Therefore, to make use of a block cipher like AES, you need to define a way of converting an arbitrary-length message into a sequence of fixed-length blocks prior to encryption. Similarly, the method has to enable you to reassemble messages from blocks during decryption. The method used to convert between messages and blocks is referred to as the block cipher's mode of operation.
There are quite a few different modes that can be used in conjunction with AES. NIST, for example, has a list of 16 different approaches on its Web site and is open for more proposals. The choice of the mode is very important because it has implications both for the complexity of implementation and also for security. Bad modes can create security loopholes even though the underlying AES encryption is so strong.
CCMP uses a mode called CCM, which itself is based on counter mode. Before looking at these modes, let's consider the issue of message authenticity. AES provides a method for encrypting data, obscuring the content so it cannot be read by an attacker. However, and just as important, the receiver needs to know that the message is authentic?that it has not been modified. This is usually accomplished by adding a message integrity code (MIC).[1] For efficiency, we want this MIC to be computed using the AES encryption algorithm so it makes sense that the operating mode should define how to provide both encryption and authenticity.
[1] The term "MAC" is widely used in cryptography, but IEEE 802.11i (and other chapters in this book) use the term MIC instead because the acronym MAC is already used.
To understand modes of operation, we start by reviewing one of the most simple and intuitive modes: Electronic Code Book (ECB). The mode is generally indicated by being placed after the letters "AES" so a system using Electronic Code Book described as AES/ECB.
Electronic Code Book (ECB)
ECB mode (Menezes et al., 1996; Schneier, 1996) simply takes a piece off the input message one block at a time and encrypts each block sequentially using the same key until no more pieces are left. This process is shown in Figure 12.1, which displays the computation for both serial (one block at a time) and parallel encryption.
Figure 12.1. ECB Operating Mode
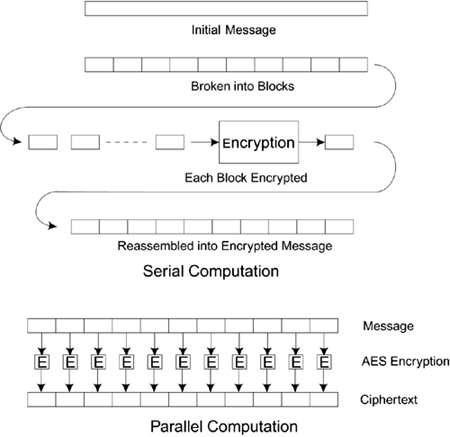
This approach sounds simple, but it has a couple of problems. The most obvious is that the message may not be an exact multiple of the block size so you have to pad out any partial block at the end and remember the real length. However, there is also a security problem: If two blocks have the same data, the encrypted result of the two blocks will also be the same, giving information to any onlooker.
Consider a message composed of a string of the same letter repeated 64 times, for example, "AAAAAAA…". If the AES block size is 128 bits (16 bytes), then using ECB would break down the message to four blocks, each with a string of 16 A's. After encryption, the four blocks would each produce identical ciphertext, informing an onlooker that this message has a repeating pattern. Because of this weakness (and others), practical systems do not use ECB. It is not, for example, on the list of NIST-recommended modes. Even the strongest block cipher cannot protect against weaknesses in the mode.
Counter Mode
Counter mode is more complicated that ECB and operates in quite a different way. It does not use the AES block cipher directly to encrypt the data. Instead, it encrypts the value of an arbitrary value called the counter and then XORs the result with the data to produce ciphertext. The counter is generally incremented by 1 for each successive block processed?hence the name. This process is shown in Figure 12.2.
Figure 12.2. Example of Counter Mode
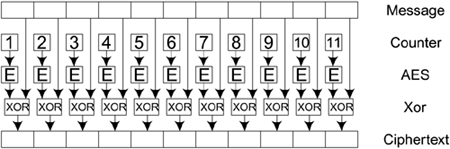
In this example the message is divided into blocks, and each block is XORed, with the result of encrypting the counter value using AES. In Figure 12.2 the counter starts at 1 and increments up to 11. In practice, the counter might start at an arbitrary value and might increment by some other value or pattern. The important thing is that the receiving party who wants to decrypt the message must know the starting value of the counter and the rules for advancing it.
Because the counter changes value for each block, the problem seen in ECB with repeating blocks is avoided. Even if two blocks of data were identical, they would be combined with a different counter value to produce different ciphertext. However, as presented, this method would still encrypt two identical, but separate, messages to the same result. This is why, in practice, the counter does not start at 1. Typically, it is initialized from a nonce value that changes for each successive message.
Counter mode has some interesting properties. Decryption is exactly the same process as encryption because XORing the same value twice takes you back to the original value.[2] This means that implementations only need to implement the AES encryption block (and not the decryption block). The other useful feature, for some applications, is that the encryption can be done completely in parallel. Because all the counter values are known at the start, you could have a bank of AES encryption devices and encrypt an entire message in a single parallel operation. This is not the case for many of the other modes. The last useful property is that there is no problem if the message doesn't break into an exact number of blocks. You simply take the last (short) block and XOR it with the encrypted counter output using only the number of bits you need. Therefore, the length of the ciphertext can be exactly the same as the length of the input message. Because each block operation depends on the state of the counter from the previous block, counter mode is essentially stream cipher.
[2] This is an example in which the underlying cipher does not need to be reversible.
Counter mode has been used for more than twenty years and is well known and trusted by the cryptographic community. Its simplicity and maturity make it an attractive option for RSN. However, basic counter mode does not provide any message authentication, only encryption. Therefore, for RSN, additional capability must be added.
Counter Mode + CBC MAC : CCM
CCM mode was created especially for use in IEEE 802.11i RSN, but it is applicable to other systems as well and has been submitted to NIST as a general mode for use with AES. It has also been submitted to the IETF for use in IP security. CCM was invented by three of the cryptographers participating in the IEEE 802.11i standards group: Doug Whiting, Russ Housley, and Niels Ferguson. It builds on top of counter mode.
CCM uses counter mode in conjunction with a message authentication method called cipher block chaining (CBC). CBC is used to produce a message integrity code (MIC). The MIC is called a message authentication code by the cryptographic community, leading to the name CBC-MAC.
CBC-MAC is another technique that has been used for many years and has been standardized internationally. For more information, see Bellare et al. (2000). It is really simple in concept:
Take the first block in the message and encrypt it using AES (or any block cipher).
XOR the result with the second block and then encrypt the result.
XOR the result with the next block and encrypt that…and so on.
The result is a single block (128 bits in our case) that combines all the data in the message. If one or more bits were to change in the message, the result would be completely different (okay, so there is a 2-128 chance it will be the same). CBC-MAC is simple but cannot be parallelized; the encryption operations must be done sequentially. Furthermore, it should be noted that, by itself, CBC-MAC can only be used on messages that are an exact number of blocks. CCMP provides a solution based on padding, as described later; however, the padding method has raised concerns among some cryptographers.
CCM mode pulls together two well-known approaches, counter mode and CBC-MAC. It adds some features that are very useful for certain applications such as RSN. The features it adds are:
Specification of a nonce so successive messages are separated cryptographically.
Linking together the encryption and authentication (message integrity) under a single key.
Extension of the authentication to cover data that is not to be encrypted.
The last item needs further explanation and is important for RSN. In most existing methods that perform both encryption and authentication, an assumption is made that the entire message will be encrypted. However, in IEEE 802.11, only part of the message needs to be encrypted. The header portion of the IEEE 802.11 frame contains the MAC addresses used to deliver the frame as well as other information relevant to operation of the Wi-Fi LAN. These fields must be sent "in the clear" so other wireless devices can operate. Therefore, only the data portion of the frame is encrypted. However, although the header is not encrypted, the receiver would still like assurance that it has not been modified. For example, you don't want an attacker to change the source address so you accidentally reply to him instead of to the original sender. To achieve this, CCM mode allows the encryption to be performed on a subpart of the message that is authenticated by CBC-MAC.
As a general rule, using the same key for two separate cryptographic functions is not wise. This rule appears to be broken here because the same key is used for both encryption and authentication. However, although the same key is used, it is in each case used in conjunction with an initialization vector (IV). The construction of the IV is different for the counter mode and CBC-MAC portions, thus leading, in effect, to two separate keys. The effectiveness of this separation has been shown by cryptographers (Jonsson, 2002).
Offset Codebook Mode (OCB)
OCB mode was invented by Phil Rogaway of the University of California, Davis, following on from work done at IBM Research Labs. It is an authenticated encryption scheme, which means it achieves both message encryption and authentication in a single computation. OCB has some advantages:
OCB is parallelizable so it can be done faster using multiple hardware blocks.
OCB is very efficient, taking only slightly more than the theoretical minimum encryption operations possible.
OCB is provably secure, which means it can be "proved" that it is as secure as the underlying block cipher (AES).
Because of its advantages, OCB was the first mode selected by the IEEE 802.11i working group and was given the name WRAP. However, concern was raised over intellectual property rights. The standards group was concerned about mandating a method that might, in the future, result in the need to make license payments. Therefore, CCMP was adopted as mandatory and OCB was eventually dropped. It is mentioned here because a few vendors have implemented WRAP, and it is possible you might encounter it as a proprietary mode in some early implementations.
If you want more details of OCB, visit Rogaway's Web site www.cs.ucdavis.edu/~rogaway or read the conference paper (Rogaway et al., 2001).







