Per-Packet Key Mixing
The key-mixing function creates a new key for every packet transmitted. It was introduced for two reasons:
As a way to protect against RC4 weak key attacks. The recommended defense (discard the first 256 bytes of key stream) was not possible in existing deployed hardware.
As a way to incorporate the extra bits of the extended IV.
The approach is to combine the session key, the IV and the source MAC address together with a hash function to produce a mixed key. Including the source MAC address provides added protection against forgery and also separates out the key space of the two communicating devices that share the session key.
Performing a hash operation for every packet to be encrypted or decrypted is a major overhead and hard work for the low-power MAC processor typical in earlier Wi-Fi LAN systems. To ease the burden, the mixing has been divided into two phases. During phase 1, the session key and source address are hashed. The result remains constant during the session. In phase 2, performed for every packet, the IV is mixed with the result of the first phase to produce an encryption key. This key is then used to initialize the RC4 encryption hardware.
Note that even the second part of the key-mixing computation can be performed in advance because the IV increases monotonically. Therefore, a station knows which values of IV will be coming up shortly and could precompute a number of keys in advance. This step avoids the need for a real-time computation when a packet is received. The two phases of key mixing are shown in Figure 11.3. As you can see in this figure, 104 bits of mixed key material are needed to form the total RC4 key of 128 bits when the IV is added.
There is nothing very glamorous about the computations for the key mixing but let's quickly look at the algorithm.
The inputs to the computation are abbreviated:
TSC = TKIP Sequence Counter (48 bits)
TSCU = Upper 32 bits of TSC (32 bits)
TSCL = Lower 16 bits of TSC (16 bits)
TA = Transmitter address, the MAC address of the encrypting station (48 bits)
TK = The temporal session key (128 bits)
P1K = Output of the first phase (80 bits)
P2K = Output of the second phase (128 bits); this becomes the RC4Key.
The two phases can be written as the following functions:
P1K
Phase1(TA, TSCU, TK)
P2K
Phase2(P1K, TSCL, TK)
When the system starts up or a new key exchange occurs, the TSC is reset to 0. The system typically computes the value of P1K right away and stores it for use in generating P2K. P1K needs to be recomputed every time TSCU changes, which is every 65536 packets. There is no reason why the next value of P1K can't be computed in advance so there will be no delay when TCSU actually changes.
Substitution Table or S-Box
Both phase 1 and phase 2 require a byte substitution table or S-box. The substitution table is to the computer what logarithm tables used to be to schoolchildren before calculators.[3] You take a value and look up a corresponding value in a table. The calculations have been done in advance to determine the correct values in the table. A typical substitution table for a byte value is 256 bytes long so there is one entry for each value of the byte.
[3] This is true for the S-box of RC-4, which is generated by computation. However, unlike log-tables, S-boxes for other algorithms may contain values that are not mathematically generated.
However, key mixing uses 16-bit word values. A full substitution table for a 16-bit value would be 216 or 65,336 words long?a total of 128Kbytes! However, this full table is needed only if you want to be able to have a reversible function and create a second table that will "undo" the substitution and get you back where you started. You do not need such a table for hashing functions; in fact, this type of reversal is something you want to prevent. Therefore, the key-mixing algorithm uses a partial substitution table with 512 word entries, which you can think of as two tables, each with 256 words. To make the substitution for a 16-bit word X, we use the upper byte of X as an index into the first table and the lower byte of X as an index into the second table. Then we exclusive OR the two words from the tables to produce a final 16-bit word substitution. This is denoted in the algorithm by the function:
i = S[j]
where i is the result of substituting for j.
The 512 values for the substitution table are listed in the standard. The same substation tables must be used by everyone for this approach to work.
Phase 1 Computation
The output of phase 1 is only 80 bits long (not 128), but it uses all 128 bits of the temporal key in the computation. The result is computed in an array of five 16-bit words called P1K0, P1K1, P1K2, P1K3, and P1K4. The following terminology is used in the algorithm:
TSC1 = bits 16?31 of the TSC (the middle 16 bits)
TSC2 = bits 32?47 of the TSC (the upper 16 bits)
TAn = nth byte of the encrypting station's MAC address
(TA0 = lowest byte, TA5 = highest byte)
TKn = nth byte of the temporal key
(TK0 = lowest byte, TK5 = highest byte)
the expression X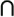
X
Y = 256*X + Y
S[ ] denotes the result from the 16-bit substitution table:
PHASE1_STEP1 P1K0 = TSC1 P1K1 = TSC2 P1K2 = TA1TA0 P1K3 = TA3
TA2 P1K4 = TA5
TA4 PHASE1_STEP2: FOR i = 0 to 3 BEGIN P1K0 = P1K0 + S[ P1K4
(TK1
TK0) ] P1K1 = P1K1 + S[ P1K0
(TK5
TK4) ] P1K2 = P1K2 + S[ P1K1
(TK9
TK8) ] P1K3 = P1K3 + S[ P1K2
(TK13
TK12) ] P1K4 = P1K4 + S[ P1K3
(TK1
TK0) ] + i P1K0 = P1K0 + S[ P1K4
(TK3
TK2) ] P1K1 = P1K1 + S[ P1K0
(TK7
TK6) ] P1K2 = P1K2 + S[ P1K1
(TK11
TK10) ] P1K3 = P1K3 + S[ P1K2
(TK15
TK14) ] P1K4 = P1K4 + S[ P1K3
(TK3
TK2) ] + 2*i + 1 END
Although this is quite a bit of computation?certainly more than in phase 2?the arithmetic comprises entirely shifts, adds, and exclusive OR operations.
Phase 2 Computation
On the face of it, phase 2 looks more complicated than phase 1. However, although there are more steps, there is no repeating loop in the computation. The result is computed in an array of six 16-bits words called: PPK0, PPK1, PPK2, PPK3, and PPK4. The following terminology is used in the algorithm:
P1Kn = output words from phase 1
TSC0 = bits 0 - 15 of the TSC (the lower 16 bits)
TKn = nth byte of the temporal key
(TK0 = lowest byte, TK5 = highest byte)
The expression X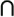
X
Y = 256*X + Y
The expression >>>(word) means that the 16-bit word is rotated one place right.
The expression 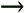
S[ ] denotes the result from the 16-bit substitution table.
RC4Keyn means the nth byte of the RC4 key used for encryption.
PHASE2,STEP1:
PPK0 = P1K0
PPK1 = P1K1
PPK2 = P1K2
PPK3 = P1K3
PPK4 = P1K4
PPK5 = P1K5 + TSC0
PHASE2,STEP2:
PPK0 = PPK0 + S[ PPK5  (TK1
(TK1 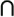 TK0) ]
PPK1 = PPK1 + S[ PPK0
TK0) ]
PPK1 = PPK1 + S[ PPK0  (TK3
(TK3 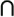 TK2) ]
PPK2 = PPK2 + S[ PPK1
TK2) ]
PPK2 = PPK2 + S[ PPK1  (TK5
(TK5 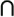 TK4) ]
PPK3 = PPK3 + S[ PPK2
TK4) ]
PPK3 = PPK3 + S[ PPK2  (TK7
(TK7 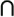 TK6) ]
PPK4 = PPK4 + S[ PPK3
TK6) ]
PPK4 = PPK4 + S[ PPK3  (TK9
(TK9 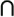 TK8) ]
PPK5 = PPK5 + S[ PPK4
TK8) ]
PPK5 = PPK5 + S[ PPK4  (TK11
(TK11 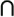 TK10) ]
PPK0 = PPK0 + >>>(PPK5
TK10) ]
PPK0 = PPK0 + >>>(PPK5  (TK13
(TK13 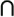 TK12))
PPK1 = PPK1 + >>>(PPK0
TK12))
PPK1 = PPK1 + >>>(PPK0  (TK15
(TK15 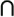 TK14))
PPK2 = PPK2 + >>>(PPK1)
PPK3 = PPK3 + >>>(PPK2)
PPK4 = PPK4 + >>>(PPK3)
PPK5 = PPK5 + >>>(PPK4)
PHASE2,STEP3:
RC4Key0 = UpperByte(TSC0)
RC4Key1 = (UpperByte (TSC0) | 0x20) & 0x7F
RC4Key2 = LowerByte(TSC0)
RC4Key3 = LowerByte ((PPK5
TK14))
PPK2 = PPK2 + >>>(PPK1)
PPK3 = PPK3 + >>>(PPK2)
PPK4 = PPK4 + >>>(PPK3)
PPK5 = PPK5 + >>>(PPK4)
PHASE2,STEP3:
RC4Key0 = UpperByte(TSC0)
RC4Key1 = (UpperByte (TSC0) | 0x20) & 0x7F
RC4Key2 = LowerByte(TSC0)
RC4Key3 = LowerByte ((PPK5 
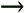 (TK1
(TK1 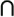 TK0))
RC4Key4 = LowerByte (PPK0)
RC4Key5 = UpperByte (PPK0)
RC4Key6 = LowerByte (PPK1)
RC4Key7 = UpperByte (PPK1)
RC4Key8 = LowerByte (PPK2)
RC4Key9 = UpperByte (PPK2)
RC4Key10 = LowerByte (PPK3)
RC4Key11 = UpperByte (PPK3)
RC4Key12 = LowerByte (PPK4)
RC4Key13 = UpperByte (PPK4)
RC4Key14 = LowerByte (PPK5)
RC4Key15 = UpperByte (PPK5)
TK0))
RC4Key4 = LowerByte (PPK0)
RC4Key5 = UpperByte (PPK0)
RC4Key6 = LowerByte (PPK1)
RC4Key7 = UpperByte (PPK1)
RC4Key8 = LowerByte (PPK2)
RC4Key9 = UpperByte (PPK2)
RC4Key10 = LowerByte (PPK3)
RC4Key11 = UpperByte (PPK3)
RC4Key12 = LowerByte (PPK4)
RC4Key13 = UpperByte (PPK4)
RC4Key14 = LowerByte (PPK5)
RC4Key15 = UpperByte (PPK5)
The final output of phase 2 is an array of 16 bytes containing the RC4 key to be used in encryption. This can be loaded into the legacy WEP encryption engine prior to processing the MPDU for transmission. The first 3 bytes of this key are transmitted as the WEP IV field (24 bits) and contain the lower 16 bits of the TKIP IV value and the TSC. The second byte of the WEP IV is a repeat of the first byte, except that bit 5 is forced to 1 and bit 4 is forced to 0. Forcing these bits prevents generation of the major class of weak keys. This byte is ignored on receipt.







