A.2 Chapter 6 Exercise Solution

Section 6.7 included only one, outrageously complicated problem. This section details the step-by-step solution to that problem.

Figure A-7 shows how to adjust effective filters to take account of join factors less than 1.0, which occur in three places in Figure 6-33.

Figure A-7. Effective filters taking account of join factors, to choose the driving table

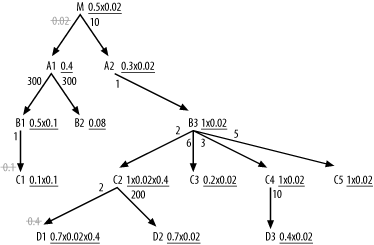
You adjust effective filters immediately on either side of the master join ratios, since you can migrate those filters upward with explicit IS NOT NULL conditions on the foreign keys. This adjusts filters on B1, C1, C2, and D1, and you cross out the master join ratios to show that you took them into account. Note the detail join ratio of 0.02 between M and A1 for even bigger adjustments on every filter from M down through the A2 branch.

If there were other branches, you would adjust them as well. Only the A1 branch, attached through that filtering join, does not see the adjustment.

Note that you adjust the effective join ratio for C2 and D1 twice, since two filtering joins affect these. Working through the numbers, you find the best effective filter, 0.004 (0.2 x 0.02), lies on C3, so that is the driving table.

After choosing the driving table, you need a whole new set of adjustments to take account of the two low master join ratios before choosing the rest of the join order. Note that you no longer need to take account of the detail join ratio, since the database is coming from the side of the join that does not discard rows through the join. This happens whenever you choose a driving table with an effective filter adjusted by the detail join ratio. In a sense, you burn the filter at the beginning, coming from smaller tables that point to only a subset of the master table (A1 in this case) on the other side of that join.

It is best to get the benefit of the hidden join filters that point to C1 and D1 as early in the join order as possible. Therefore, make explicit the is-not-null filters on the foreign keys (in B1 and C2) that point to these filtering joins, as shown in Figure A-8. By making these filters explicit (and assuming referential integrity), you no longer see filtering in the joins themselves, so you cross out those join ratios.

Figure A-8. Adjusting to make is-not-null conditions on foreign keys explicit, to optimize the rest of the join order

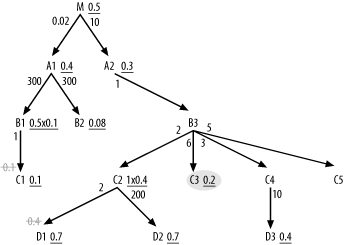
From C3, you can join only to B3, so it is next in the join order. From these two, you can join to C2, C4, C5 (below), or A2 (above). Normally, you would consider joining only next to the tables below, but notice that the detail join ratio to A2 is 1.0, so it is eligible early and, in fact, it turns out to have the best effective filter of the choices, so you join to it next. This adds M to the list of nodes now in reach, but the detail join ratio to M is high, so postpone that join as long as possible. The only eligible node below with a filter is now C2, thanks to the now-explicit not-null condition on the foreign key that points to D1, so join to C2 next. The join order, so far, is (C3, B3, A2, C2).

The join to C2 adds D1 and D2 to the list of eligible nodes downward from the joined tables so far, and these are the only eligible tables in that direction with filters, so choose one of them next. The filter ratios are identical, so look at other considerations to break the tie and note that D2 must be smaller, since the detail join ratio above it is much larger. Therefore, following the smaller-table-first tiebreaker, join to D2 before D1. The join order, so far, is (C3, B3, A2, C2, D2, D1).

Between C4 and C5, you also have a tie on filter ratios (unshown) equal to 1.0, but you break the tie with the filter-proximity rule that favors C4 for the path it provides to the filter on D3. After reaching C4, go to D3 for that filter and finally join to the unfiltered C5. The join order, so far, is (C3, B3, A2, C2, D2, D1, C4, D3, C5).

From here, there is no choice in the next node, the upward join to M. After reaching M, there is again no choice; A1 is the only node attached. At this point, you could join to either B1 or B2. Their filter ratios are nearly a tie for purposes of later joins, but their detail join ratios are the same, so they should be the same size, leaving table size out of the picture. You can also leave proximity out of the picture, because the filter on C1 is no better than the filter on B1. With no reason to override going to the best filter, on B1, you choose to join to it next. This leaves the join order, so far, of (C3, B3, A2, C2, D2, D1, C4, D3, C5, M, A1, B1). The only two nodes left, B2 and C1, are both eligible now. B2 has the better filter, and the combination of master join ratio and detail join ratio to C1 shows it to be 1/10th the size of B1. B1, in turn, was the same size as B2, so B2 and C1 are different in size by a factor of 10, probably enough for the smaller-table-first tiebreaker rule to favor C1 in the near-tie between B2 and C1. Therefore, go with C1 first, leaving the complete join order of (C3, B3, A2, C2, D2, D1, C4, D3, C5, M, A1, B1, C1, B2).

These last few joins actually will affect the query cost very little, since the query will be down to a few rows by this point.

To reach the root table from C3, for a robust nested-loops plan, the database needs foreign-key indexes (from M to A2, from A2 to B3, and from B3 to C3) on M, A2, and B3. You probably need no index at all on C3, since the 20% filter on that table is not selective enough to make an index outperform a full table scan. (This is probably a small table, based on the join factors.) All other tables require indexes on their primary keys to enable a robust plan.

To make the hidden join filters to C1 and D1 explicit and apply them earlier in the plan, add the conditions C2.FkeyToD1 IS NOT NULL AND B1.FkeyToC1 IS NOT NULL to the query.

Now, relax the robust-plan requirement, and work out which joins should be hash joins and which access path should be used for the hash-joined tables. Recall that table A1 has 30,000,000 rows. From the detail join ratios, B1 and B2 have 1/300^th as many rows: 100,000 each. From the combination of master join ratio and detail join ratio, C1 has 1/10^th as many rows as B1: 10,000. Going up from A1 to M, M has far fewer (0.02 times as many) rows as A1: 600,000. Coming down from M, using detail join ratios, calculate 60,000 for A2 and B3, 30,000 for C2, 10,000 for C3, 20,000 for C4, and 12,000 for C5. Using both master and detail join ratios from C2 to D1, calculate 6,000 (30,000 x 0.4/2) rows for D1. From detail join ratios, find 150 rows in D2 and 2,000 rows in D3.

Any part of the plan that reads more rows from a table than the database would read using the filter on that table tends to favor accessing that table through the filter index and using a hash join at the same point in the original execution plan. Any part of the plan that reads at least 5% of the rows in a table tends to favor a full table scan of that table with a hash join. When both sorts of hash-join access are favored over nested loops (i.e., for a hash join with an indexed read of the filter or with a full table scan), favor the full table scan if the filter matches at least 5% of the table.

As discussed in Chapter 2, the actual cutoff for indexed access can be anywhere between 0.5% and 20%, but this exercise stated 5% as the assumed cutoff, to make the problem concrete.

In summary, Table A-1 shows the table sizes and full-table-scan cutoffs, arranged in join order.

Now, working out the rowcounts at each stage of the query, you find that, after the full table scan to C3, the filter on C3 drops the rowcount to 2,000 rows. Joining upward with nested loops to B1 touches 12,000 rows of that table, since the detail join ratio is 6. B3 has no filter, so following the one-to-one (on average) join to A2 also reaches 12,000 rows, after which the filter on A2 leaves 30% (3,600 rows) for the next join to C2. With an implied master join ratio of 1.0, nested loops would touch 3,600 rows of C2. The filters on C2 (including the now-explicit is-not-null filter on the foreign key to D1) reduce that rowcount to 1,440 before the join to D2. Nested loops to D2 read 1,440 rows of that table, after which the filter leaves 1,008 rows. Nested loops to D2 read 1,008 rows of that table (since by this point all rows have nonnull foreign keys that point to D1), after which the filter leaves 706 rows (rounding, as I will for the rest of the calculation).

Nested loops to C4 read 706 rows of that table, which are unfiltered, leaving 706. Nested loops to D3 read 706 rows of that table, after which the filter leaves 282. Nested loops to C5 read 282 rows of that table, which are unfiltered, leaving 282. With the detail join ratio of 10, the join upward into M reaches 2,820 rows of that table, after which the filter leaves 1,410. With the implied master join ratio of 1.0, nested loops reach 1,410 rows of the biggest table, A1, after which the filter leaves 564. Nested loops to B1 read 564 rows of that table, after which the filters (including the now-explicit foreign-key-is-not-null condition on the key on B1 that points to C1) leave 28. Nested loops to C1 read 28 rows of that table (since by this point all rows have nonnull foreign keys that point to C1), after which the filter leaves 3. Nested loops to B2 read 3 rows of that table, after which the final filter leaves 0 or 1 row in the final result.

If you compare these counts of rows reached by nested loops with the full-table-scan cutoffs, you see that hash joins to full table scans reduce cost for several of the tables. Since none of the filters in this query were selective enough to prefer single-table indexed access to full table scans (by the assumed 5% cutoff), you would choose hash joins to rowsets read by full table scans, when you choose hash joins at all. This example shows an unusually favorable case for hash joins. More common examples, with queries of large tables that have at least one selective filter, show fractionally much smaller improvements for hash joins to the smallest tables only.

Table A-2 shows the rowcounts calculated for the best robust plan, alongside the cutoff rowcounts that would result in a hash join to a full table scan being faster. The rightmost column, labeled Method/Join, shows the optimum table access and join methods that result for each table in the leftmost column.

Note that replacing nested-loops joins with hash joins as shown eliminates the need (for this query, at least) for the foreign-key indexes on B3 and A2 and the primary-key indexes on C2, D2, D1, and D3.