A.3 Chapter 7 Exercise Solution
Section 7.5 included only one problem, which was deliberately very complex to exercise most of the subquery rules. This section details the step-by-step solution to that problem. Figure A-9 shows the missing ratios for the three semi-joins and the anti-join.
Figure A-9. The diagram from Figure 7-36, with the missing subquery ratios filled in
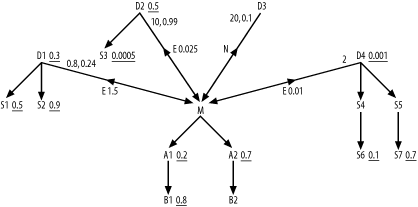
I'll begin by reviewing the calculation of the missing ratios shown in Figure A-9. To find the correlation preference ratio for the semi-join to D1, follow the rules stated in Chapter 7, in Section 7.2.1.1. In Step 1, you find that the detail join ratio for D1 from Figure 7-36 is D=0.8. This is an uncommon case of a many-to-one join that averages less than one detail per master row. Assume M=1, the usual master join ratio when it is not explicitly shown on the diagram. The best filter ratio among the nodes of this subquery (D1, S1, and S2) is 0.3 on D1, so S=0.3. The best filter ratio among the nodes of the outer query (M, A1, A2, B1, and B2) is 0.2 for A1, so R=0.2. For Step 2 of the rules, find D x S=0.24 and M x R=0.2, so D x S>M x R. Therefore, proceed to Step 3. You find S>R, so you set the correlation preference ratio to S/R=1.5, next to the semi-join indicator E from M to D1.
To find the correlation preference ratio for the semi-join to D2, repeat the process. In Step 1, you find the detail join ratio from Figure 7-36 (D=10). Assume M=1, the usual master join ratio when it is not explicitly shown on the diagram. The best filter ratio between D2 and S3 is 0.0005 on S3, so S=0.0005. The best filter ratio among the nodes of the outer query, as before, is R=0.2. For Step 2 of the rules, find D x S=0.005 and M x R=0.2, so D x S<M x R. Therefore, Step 2 completes the calculation, and you set the correlation preference ratio to (D x S)/(M x R)=0.025, next to the semi-join indicator E from M to D2.
To find the correlation preference ratio for the semi-join to D4, repeat the process. In Step 1, you find that the detail join ratio from Figure 7-36 is D=2. Assume M=1, the usual master join ratio when it is not explicitly shown on the diagram. The best filter ratio among D4, S4, S5, S6, and S7 is 0.001 on D4, so S=0.001. The best filter ratio among the nodes of the outer query, as before, is R=0.2. For Step 2 of the rules, find D x S=0.002 and M x R=0.2, so D x S<M x R. Therefore, Step 2 completes the calculation, and you set the correlation preference ratio to (D x S)/(M x R)=0.01, next to the semi-join indicator E from M to D4.
Now, shift to the next set of rules, to find the subquery adjusted filter ratios. Step 1 dictates that you do not need a subquery adjusted filter ratio for D4, because its correlation preference ratio is both less than 1.0 and less than any other correlation preference ratio. Proceed to Step 2 for both D1 (which has a correlation preference ratio greater than 1.0) and D2 (which has a correlation preference ratio greater than D4's correlation preference ratio). The subqueries under both D1 and D2 have filters, so proceed to Step 3 for both. For D1, find D=0.8 and s=0.3, the filter ratio on D1 itself. At Step 4, note that D<1, so you set the subquery adjusted filter ratio equal to s x D=0.24, placed next to the 0.8 on the upper end of the semi-join link to D1.
At Step 3 for D2, find D=10 and s=0.5, the filter ratio on D2 itself. At Step 4, note that D>1, so proceed to Step 5. Note that s x D=5, which is greater than 1.0, so proceed to Step 6. Set the subquery adjusted filter ratio equal to 0.99, placed next to the 10 on the upper end of the semi-join link to D2.
The only missing ratio now is the subquery adjusted filter ratio for the anti-join to D3. Following the rules for anti-joins, for Step 1, find t=5 and q=50 from the problem statement. In Step 2, note that there is (as with many NOT EXISTS conditions) just a single node in this subquery, so C=1, and calculate (C-1+(t/q))/C=(1-1+(5/50))/1=0.1.
Now, proceed to the rules for tuning subqueries, with the completed query diagram. Following Step 1, ensure that the anti-join to D3 is expressed as a NOT EXISTS correlated subquery, not as a noncorrelated NOT IN subquery. Step 2 does not apply, because you have no semi-joins (EXISTS conditions) with midpoint arrows that point downward. Following Step 3, find the lowest correlation preference ratio, 0.01, for the semi-join to D4, so express that condition with a noncorrelated IN subquery and ensure that the other EXISTS-type conditions are expressed as explicit EXISTS conditions on correlated subqueries. Optimizing the subquery under D4 as if it were a standalone query, you find, following rules for simple queries, the initial join order of (D4, S4, S6, S5, S7). Following this start, the database will perform a sort-unique operation on the foreign key of D4 that points to M across the semi-join. Nested loops follow to M, following the index on the primary key of M. Optimize from M as if the subquery condition on D4 did not exist.
Step 4 does not apply, since you chose to drive from a subquery IN condition. Step 5 applies, because at node M you find all three remaining subquery joins immediately available. The semi-join to D1 acts like a downward-hanging node with filter ratio of 0.24, not as good as A1, but better than A2. The semi-join to D2 acts like a downward-hanging node with a filter ratio of 0.99, just better than a downward join to an unfiltered node, but not as good as A1 or A2. The anti-join to D3 is best of all, like many selective anti-joins, acting like a downward-hanging node with a filter ratio of 0.1, better than any other.
Therefore, perform the NOT EXISTS condition to D3 next, and find a running join order of (D4, S4, S6, S5, S7, M, D3). Since the subquery to D3 is single-table, return to the outer query and find the next-best downward-hanging node (or virtual downward-hanging node) at A1. This makes B1 eligible to join, but B1 is less attractive than the best remaining choice, D1, with its subquery adjusted filter ratio of 0.24, so D1 is next. Having begun that subquery, you must finish it, following the usual rules for optimizing a simple query, beginning with D1 as the driving node. Therefore, the next joins are S1 and S2, in that order, for a running join order of (D4, S4, S6, S5, S7, M, D3, A1, D1, S1, S2).
Now, you find eligible nodes A2, B1, and D2, which are preferred in that order, based on their filter ratios or (for D2) their subquery adjusted filter ratio. When you join to A2, you find a new eligible node, B2, but it has a filter ratio of 1.0, which is not as attractive as the others. Therefore, join to A2, B1, and D2, in that order, for a running join order of (D4, S4, S6, S5, S7, M, D3, A1, D1, S1, S2, A2, B1, D2). Having reached D2, you must complete that subquery with the join to S3, and that leaves only the remaining node B2, so the complete join order is (D4, S4, S6, S5, S7, M, D3, A1, D1, S1, S2, A2, B1, D2, S3, B2).






