9.1 Outer Joins
In one sense, this section belongs in Chapter 6 or Chapter 7, because in many applications outer joins are as common as inner joins. Indeed, those chapters already cover some of the issues surrounding outer joins. However, some of the questions about outer joins are logically removed from the rest of the tuning problem, and the answers to these questions are clearer if you understand the arguments of Chapter 8. Therefore, I complete the discussion of outer joins here.
Outer joins are notorious for creating performance problems, but they do not have to be a problem when handled correctly. For the most part, the perceived performance problems with outer joins are simply myths, based on either misunderstanding or problems that were fixed long ago. Properly implemented, outer joins are essentially as efficient to execute as inner joins. What's more, in manual optimization problems, they are actually easier to handle than inner joins.
Justification of Outer JoinsI often hear discussions of outer joins that follow lines like this: "Justify making this join an outer join: prove that the expense of an outer join is necessary, here." Since I find no expense in correctly implemented outer joins, I tend to ask the opposite: "Why use an inner join when the outer case of the outer join might be useful?" Specifically, when I find unfiltered leaf nodes in a query diagram, I suspect that the join ought to be an outer join. Whole branches of join trees should often be outer-joined to the rest of the query diagram when those branches lack filters. As I mention in Chapter 7, filtered nodes generally exclude the outer case of an outer join. By making these effectively inner joins explicitly inner, you increase the degrees of freedom in the join order, which can give the optimizer access to a better execution plan. Inner joins to nodes without filters can also serve a subtle filtering role, when the master join ratio to those nodes is even slightly less than 1.0. When this filtering effect is functionally necessary, the inner join is essential. However, it is far more common that this subtle filtering effect was the farthest thing from the developer's mind when she was writing the SQL. More commonly, the filtering effect of an inner join to a node without filters is unintentional and undesirable. Even when the foreign key is nonnull and the join will produce the outer case only when referential integrity fails, ask yourself "Would it be better to show the rows with failed referential integrity, or to hide them?" Failed referential integrity is a problem whether you see it or not, so I argue for using outer joins to reveal such a failure to the end user and give developers or DBAs a chance to learn of the defect, as the first step to repairing it. |
I already discussed several special issues with outer joins in Chapter 7, under sections named accordingly:
Filtered outer joins
Outer joins leading to inner joins
Outer joins pointing toward the detail table
Outer joins to views
These cases all require special measures already described in Chapter 7. Here, I extend the rules given in Chapter 7 to further optimize the simplest, most common case: simple, unfiltered, downward outer joins to tables, either nodes that are leaf nodes of the query diagram or nodes that lead to further outer joins. Figure 9-1 illustrates this case with 16 outer joins.
Figure 9-1. A query with 16 unfiltered outer joins
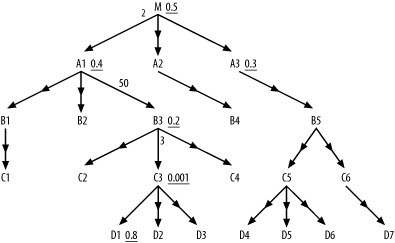
I call these unfiltered, downward outer joins to simple tables normal outer joins. Normal outer joins have a special and useful property, from the point of view of optimization:
The number of rows after performing a normal outer join is equal to the number of rows just before performing that join.
This property makes consideration of normal outer joins especially simple; normal outer joins have no effect at all on the running rowcount (the number of rows reached at any point in the join order). Therefore, they are irrelevant to the optimization of the rest of the query. The main justification for performing downward joins before upward joins does not apply; normal outer joins, unlike inner joins, cannot reduce the rowcount going into later, more expensive upward joins. Since they have no effect on the rest of the optimization problem, you should simply choose a point in the join order where the cost of the normal outer join itself is minimum. This turns out to be the point where the running rowcount is minimum, after the first point where the outer-joined table is reachable through the join tree.
9.1.1 Steps for Normal Outer Join Order Optimization
The properties of normal outer joins lead to a new set of steps specific to optimizing queries with these joins:
Isolate the portion of the join diagram that excludes all normal outer joins. Call this the inner query diagram.
Optimize the inner query diagram as if the normal outer joins did not exist.
Divide normal outer-joined nodes into subsets according to how high in the inner query diagram they attach. Call a subset that attaches at or below the driving table s_0; call the subset that can be reached only after a single upward join from the driving table s_1; call the subset that can be reached only after two upward joins from the driving table s_2; and so on.
Work out a relative running rowcount for each point in the join order just before the next upward join and for the end of the join order.
Call the relative running rowcount just before the first upward join r_0; call the relative running rowcount just before the second upward join r_1; and so on. Call the final relative rowcount r_j, where j is the number of upward joins from the driving table to the root detail table.
|
For each subset s_n, find the minimum value r_m (such that m
n) and join all the nodes in that subset, from the top down, at the point in the join order where the relative rowcount equals that minimum. Join the last subset, which hangs from the root detail table, at the end of the join order after all inner joins, since that is the only eligible minimum for that subset.
9.1.2 Example
These steps require some elaboration. To apply Steps 1 and 2 to Figure 9-1, consider Figure 9-2.
Figure 9-2. The inner query diagram for the earlier query
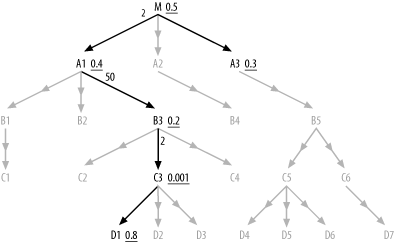
The initially complex-looking 22-way join is reduced in the inner query diagram in black to a simple 6-way join, and it's an easy optimization problem to find the best inner-join order of (C3, D1, B3, A1, M, A3).
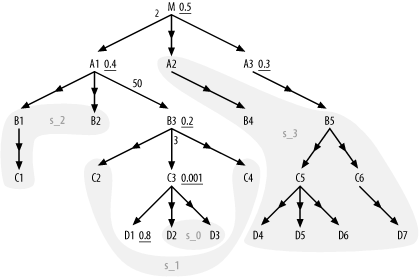
Now, consider Step 3. The driving table is C3, so the subset s_0 contains any normal outer-joined tables reachable strictly through downward joins hanging below C3, which would be the set {D2, D3}. The first upward join is to B3, so s_1 is {C2, C4}, the set of nodes (excluding s_0 nodes) reachable through downward joins from B3. The second upward join is to A1, so s_2 is {B1, B2, C1}. The final upward join is to M, so s_3 holds the rest of the normal outer-joined tables: {A2, B4, B5, C5, C6, D4, D5, D6, D7}. Figure 9-3 shows this division of the outer-joined tables into subsets.
Figure 9-3. The outer-joined-table subsets for the earlier query
Now, consider Step 4. Since you need only comparative (or relative) running rowcounts, let the initial number of rows in C3 be whatever it would need to be to make r_0 a convenient round numbersay, 10. From there, work out the list of values for r_n:
- r_0: 10
-
Arbitrary, chosen to simplify the math.
- r_1: 6 (r_0 x 3 x 0.2)
-
The numbers 3 and 0.2 come from the detail join ratio for the join into B3 and the product of all filter ratios picked up before the next upward join. You would also adjust the rowcounts by master join ratios less than 1.0, if there were any, but the example has only the usual master join ratios assumed to be 1.0. (Since there are no filtered nodes below B3 reached after the join to B3, the only applicable filter is the filter on B3 itself, with a filter ratio of 0.2.)
- r_2: 120 (r_1 x 50 x 0.4)
-
The numbers 50 and 0.4 come from the detail join ratio for the join into A1 and the product of all filter ratios picked up before the next upward join. (Since there are no filtered nodes below A1 reached after the join to A1, the only applicable filter is the filter on A1 itself, with a filter ratio of 0.4.)
- r_3: 36 (r_2 x 2 x 0.15)
-
The numbers 2 and 0.15 come from the detail join ratio for the join into M and the product of all remaining filter ratios. (Since there is one filtered node reached after the join to M, A3, the product of all remaining filter ratios is the product of the filter ratio on M (0.5) and the filter ratio on A3 (0.3): 0.5 x 0.3=0.15.)
Finally, apply Step 5. The minimum for all relative rowcounts is r_1, so the subsets s_0 and s_1, which are eligible to join before the query reaches A1, should both join at that point in the join order just before the join to A1. The minimum after that point is r_3, so the subsets s_2 and s_3 should both join at the end of the join order. The only further restriction is that the subsets join from the top down, so that lower tables are reached through the join tree. For example, you cannot join to C1 before you join to B1, nor to D7 before joining to both B5 and C6. Since I have labeled master tables by level, Ds below Cs, Cs below Bs, Bs below As, you can assure top-down joins by just putting each subset in alphabetical order. For example, a complete join order, consistent with the requirements, would be: (C3, D1, B3, {D2, D3}, {C2, C4}, A1, M, A3, {B1, B2, C1}, {A2, B4, B5, C5, C6, D4, D5, D6, D7}), where curly brackets are left in place to show the subsets.







