13.1 Hashing Algorithms Explained
A hashing algorithm creates a hash code, also called a "message digest" or "message fingerprint." As we explained in Chapter 12, hash codes are of limited use for communications security, because Eve can replace both the hash code and the message that Bob receives, but they are an essential element of digital signatures, which we discuss in Chapter 16.
In this section, we explain how hashing algorithms work, and provide some practical insight into choosing a suitable algorithm for your project.
13.1.1 Creating a Hash Code
At the heart of a hashing algorithm is a mathematical function that operates on two fixed-size blocks of data to create a hash code, as shown in Figure 13-1.
Figure 13-1. The hash function operates on fixed-size blocks of data

We break up Alice's message into blocks that are the same size as the input for the hash function. The size of each data block varies depending on the algorithm but the blocks tend to be smallthe algorithms included in the .NET Framework break the messages into blocks of 512 or 1024 bits. The design of the hash function differs for each hashing algorithm, but they all share the same basic approach.
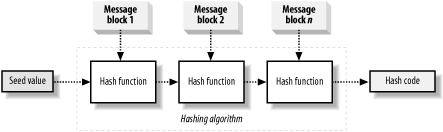
The algorithm specifies a "seed" value that feeds into the hash function along with the first block of message data, thus producing our first hash code. Take this hash code and feed it into the hash function along with the second block of message data, creating a second hash code. Feed the second hash code into the function along with the third message block, and repeat the process of hashing a data block along with the hash code of the previous block until you have processed all of the message data, as shown in Figure 13-2.
Figure 13-2. Creating the hash code by "chaining" the hash function
The idea of a hash code acting as a message "fingerprint" is reasonable, because making even the smallest change in the message data changes the value of the final hash code. By "chaining" repeated calls to the hashing function, you can create a hash code that relies on the value of every single bit of the message. The output of hashing the first data block becomes an input to the next operation, which will alter the value of the second hash code, which will affect the result of the third operation, and so on. Known as a "ripple effect" or an "avalanche," the huge impact that the smallest change has on the final hash code provides the fingerprint. Two messages that differ by a single bit of data produce very different hash codes.
It is important not to confuse the hashing algorithm with the hash function. The hash function generates a hash code by operating on two blocks of fixed-length binary data. The hashing algorithm describes the process of using the hash function to create a hash code for a messagethe algorithm is a protocol for using the hash function, specifying how the message will be broken up and how the results from previous message blocks are chained together.
13.1.2 Message Limits
There is limit to the size of message that a hashing algorithm can process before the hash code is no longer secure. A very large message causes the initial bytes of message data to have less of an effect on the hash code than the bytes at the end of the message. This means that it is easier for Eve to find a message with the same hash code as Alice sent to Bob, because we have increased the likelihood of being able to find two messages with slightly different initial bytes that result in the same hash code.
The problem arises because the hash function is called so many times for large messagesfor example, a 1 GB message will cause the hash function to be called more than 6,000,000 times. So many hashing operations lessen the "ripple effect."
Most hashing algorithms impose a message size limit of 264 bits. This limit is not a practical consideration for most projects but can be an issue when calculating hash codes for data generated over a long period. Some algorithms are able to process 2128 bits of data securely.
All of the hashing algorithms in the .NET Framework can handle message limits of at least 264 bits, which is sufficient for most projects. However, we recommend that you bear the limit in mind when considering hashing algorithms provided by third parties.
13.1.3 Hash Code Length
It is common to refer to a hash code as "uniquely" identifying a message, but the reality is slightly different. The reason that hash codes can be used to protect message integrity is that it is very difficult (but not impossible) to find another message that produces the same hash code.
Irrespective of the size or content of the message processed, hash algorithms produce a fixed-length hash code, meaning that there is a finite set of hash code values. We measure the length of a hash code in binary bits, meaning that a 64-bit hash code can represent 264 different numeric hash values.
You can create an infinite number of different messages, and there are only a finite number of possible hash codes; therefore, it must be possible to find a pair of messages that produce the same hash code. In this section, we consider the security of a 64-bit hash code which was, until quite recently, thought of as very secure.
For Eve to find a message that produces the same hash code that Alice has sent to Bob, we expect that she will have to create and test 264 (18,446,744,073,709,551,616) different messages before she finds a match (assume that hash codes are evenly distributed). If Eve can check 50 messages per second (around what you can achieve using our desktop PCs), then it will take her 11.6 billion years to test enough messages. If Eve were able to access very powerful computers, she might be able to check 10 million messages each second, but we would still expect her to take 58,494 years to find a match. This is the basic security of hash codes; realistically, Eve cannot wait almost 60,000 years, meaning that finding a matching message for a specific hash code is "computationally infeasible"a phrase that is used by cryptographers to mean "possible, but extremely unlikely."
However, if Eve can control the contents of both messages, then she has a much easier job of finding two matching hash codes, known as a message collision. If Eve wants to find any pair of messages that create the same hash code, then she only has to create and test 232 different messages before she has a better than 50% chance of finding two that match. In fact, if she is able to check 50 messages a second, she is likely to find a match in less than 3 years, which is a lot less than the 11.6 billion years it would take to handle 264 messages. If Eve is able to check 10 million messages per second, she is likely to find a pair of messages in a little over 7 minutes.
Eve now has a pair of messages that she has written, both of which result in the same hash code. She cannot use these messages to bother Alice and Bob, because she is unlikely to get Alice to hash either of her messages and send them to Bob. However, Eve can use the following attack to defraud Joe, who happens to owe her some money:
Eve creates two versions of a message. The first message instructs Joe's bank to pay Eve $100, which is the amount he owes her. The second message instructs Joe's bank to pay Eve $1,000,000.
Eve generates 232 variations of the innocuous message by making minor editorial changes that do not affect the meaning of the message (for example, adding spaces or tabs, or altering the formatting).
Eve also generates 232 variations of her dishonest message. Because she is in control of the content of both messages, the chances of her finding a version of the innocuous message and the dishonest message with the same hash code are better than 50%.
Eve sends the innocuous message to Joe, who creates a hash code and digitally signs it (see Chapter 16 for more information about digital signatures). Joe sends the signed hash code to Eve so that she may present the signed message to his bank.
Eve presents her dishonest message to Joe's bank along with the signed hash code. The bank checks the digital signature and finds that the hash code matches the message and that Joe signed it. Eve was able to forge a signature without learning Joe's secret keys.
Luckily, for Joe at least, most banks would not honor a request for a million dollars in this way. Nonetheless, Eve was able to create a forged message with very little effortin fact, if Joe has used a 64-bit hash code for his signature, it would have taken Eve somewhere between 7 minutes and 3 years to create the messages. Looking for collisions in this way is a "birthday" attack and drastically reduces the effectiveness of a hashing algorithm, forcing you to treat a hash code as though it was only half of its actual length.
Birthday AttacksHow many people must be in a room before the probability of one of them sharing your birthday is greater then 50%? The answer is 183. How many people have to be in the room before the probability of any two people sharing the same birthday is greater than 50%? The answer is 23. It is easier to find any shared birthday than to find a specific one. Eve is relying on being able to create two messages that produce the same hash code, knowing that it is simpler than trying to find a match for a specific message from Alice. Any attack along these lines is a "birthday attack." |
If this kind of attack is possible in your project, then you will need to select an algorithm that creates hash codes with twice the length you might expect. If this kind of attack is not possible, then you should select a hash code based on its actual length. As a rule, a longer hash code will take more time to attack, but takes longer to generate.
13.1.4 The .NET Framework Hashing Algorithms
The .NET Framework includes classes for five different hashing algorithms, although four of them are closely related, being variations of the same basic premise to create hash codes of different length. Table 13-1 lists the hashing algorithms available.
|
Name |
Input block size |
Message limit (bits) |
Hash code size (bits) |
|---|---|---|---|
|
MD5 |
512 |
264 |
128 |
|
SHA-1 |
512 |
264 |
160 |
|
SHA-256 |
512 |
264 |
256 |
|
SHA-384 |
1024 |
2128 |
384 |
|
SHA-512 |
1024 |
2128 |
512 |
Developed in 1991, MD5 has been used in all sorts of systems and is an integral part of many standards for communications security. MD stands for "Message Digest," and MD5 was the fifth such algorithm that Rivest had designed.
MD5 is the fastest hashing algorithm included in the .NET Framework, but the relatively small hash code size makes it more susceptible to brute force and birthday attacks.
The National Security Agency (NSA) designed the Secure Hash Algorithm (SHA) in 1993, and the National Institute of Standards and Technology (NIST) published it as Federal Information Processing Standard (FIPS) 180, permitting its use in government projects. NSA withdrew the standard shortly after publication, replacing it with SHA-1, which contained a slight modification to the hash function.
The NSA stated that the change addressed a flaw in the original algorithm that reduced its cryptographic security. The NSA has never described this flaw, leading the paranoid world of cryptographers to spend many thousands of hours analyzing the algorithm, looking for any weaknesses deliberately introduced into SHA-1 to facilitate government skullduggery. To date, no weaknesses have been found, and SHA-1 is considered a secure algorithm.
NIST published FIPS 180-2 in 2001, which defined the SHA-256, SHA-384, and SHA-512 algorithms, named after the length of the hash code that each produces. These new algorithms are variations of SHA-1, but are sufficiently recent that their cryptographic security remains open.
Consider how much you know about an algorithm before selecting one for use in a project. For example, although SHA-256, SHA-384, and SHA-512 have longer hash codes, MD5 and SHA-1 are tried and tested and are known to be reliable. Remember that a longer hash code does not provide greater security if the underlying algorithm is flawed.







