15.1 Asymmetric Encryption Explained

Asymmetric encryption, often called "public key" encryption, allows Alice to send Bob an encrypted message without a shared secret key; there is a secret key, but only Bob knows what it is, and he does not share it with anyone, including Alice. Figure 15-1 provides an overview of this asymmetric encryption, which works as follows:

Figure 15-1. Asymmetric encryption does not require Alice and Bob to agree on a secret key

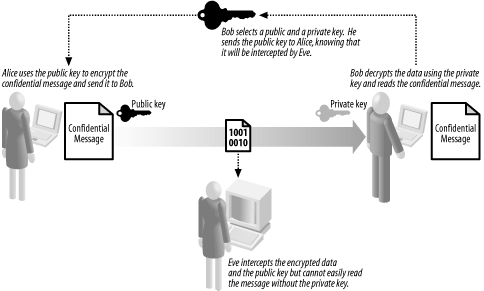
Bob creates a pair of keys, one of which he keeps secret and one of which he sends to Alice.
Alice composes a confidential message and encrypts it using the key that Bob has sent to her.
Alice sends the encrypted data to Bob.
Bob uses his secret key to decrypt the data and reads the confidential message.

The key that Bob sends to Alice is the public key, and the key he keeps to himself is the "private" key; jointly, they form Bob's "key pair."

The most striking aspect of asymmetric encryption is that Alice is not involved in selecting the key: Bob creates a pair of keys without any input or agreement from Alice and simply sends her the public key. Bob retains the private key and keeps it secret. Alice uses an asymmetric algorithm to encrypt a message with Bob's public key and sends him the encrypted data, which he decrypts using the private key.

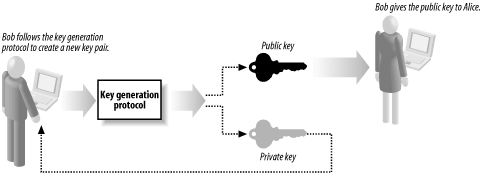
Asymmetric algorithms include a "key generation" protocol that Bob uses to create his key pair, as shown by Figure 15-2. Following the protocol results in the creation of a pair of keys that have a mathematical relationshipthe exact detail of the protocol and the relationship between the keys is different for each algorithm.

Figure 15-2. Bob uses a key generation protocol to create a new key pair

When we talk about an asymmetric encryption algorithm, we are actually referring to two related functions that perform specific tasks: an encryption function that encrypts a message using a public key, and a decryption function that uses a secret key to decrypt a message encrypted with the corresponding public key.

The encryption function can only encrypt data. Alice cannot decrypt ciphertext that she has created using the encryption function. This means that Bob can send his public key to several people, and each of them can create ciphertext that only Bob's secret key can decrypt, as shown in Figure 15-3.

Figure 15-3. Alice and Anthony are able to use the same public key to create ciphertext that can only be decrypted using Bob's secret key

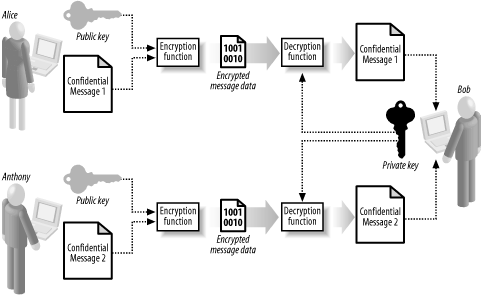
The one-way nature of the encryption function means that messages created by one sender cannot be read by another (i.e., Alice cannot decrypt the ciphertext that Anthony has created, even though they both have Bob's public key). Bob can give out the public key to anyone who wants to send him a message, and he can even print his public key on his business card and hand it out to anyone who might want to send him a message. He can add the public key to an Internet directory of keys, allowing people Bob has never met to create messages that only he can read.

If Bob suspects that Eve has guessed his private key, he simply creates a new key pair and sends out the new public key to anyone who might send him a message. This is a lot easier than arranging to meet in a secure location to agree on a new symmetric secret key with every person that might want to communicate with him. In practice, the process of changing key pairs is more complex, and we have more to say on this topic in Chapter 17.

Bob's pair of keys allows Alice to send him encrypted messages, but Bob cannot use them to send a message back to Alice because of the one-way nature of the encryption and decryption functions. If Bob needs to send Alice a confidential message, Alice must create her own pair of keys and send the public key to Bob, who can then use the encryption function to create ciphertext that only Alice can decrypt with her private key.

The main limitation of public key encryption is that it is very slow relative to symmetric encryption and is not practical for encrypting large amounts of data. In fact, the most common use of public key encryption is to solve the key agreement problem for symmetric encryption algorithms, which we discuss in more detail in Chapter 17.

In the following sections, we demonstrate how an asymmetric encryption algorithm works. We use the RSA algorithm for our illustration because it is the only one implemented in the .NET Framework. Ronald Rivest, Adi Shamir, and Leonard Adleman created the RSA algorithm in 1977, and the name is the first letter of each of the inventors' last names. The RSA algorithm is the basis for numerous security systems, and remains the most widely used and understood asymmetric algorithm.

15.1.1 Creating Asymmetric Keys

Most asymmetric algorithms use keys that are very large numbers, and the RSA algorithm is no exception. In this section, we demonstrate the RSA key generation protocol and provide you with some general information about the structure and usage of asymmetric keys.

We step through the RSA key generation protocol, using small test values. The protocol is as follows:

Choose two large random prime numbers, p and q, of equal length and multiply them together to create n, the RSA key modulus.
Select p as 23 and q as 31, so that the modulus, n, is:
n = p x q = 23 x 31 = 713
Randomly choose e, the public exponent, so that e and (p - 1)(q - 1) are relatively prime.
Numbers are "relatively" prime when they share no common factors except 1. For these test values select a value for e that has no common factors with 660. Select e as 19.
Compute the private exponent, d, where d = e^-1mod((p - 1)(q - 1)).
For our example, we calculate d as follows:
d = 19^-1mod(22 x 30) = 139
The public key consists of e and n. The private key is d. Discard p and q, but do not reveal their values.

You can see how simple it is to create an RSA key pair. Bob sends the value of e (19) and n (713) to Alice and keeps the value of d (139) secret. Most asymmetric encryption algorithms use a similar approach to key generation; we explain the protocol for a different asymmetric algorithm in Section 15.3.

Random Prime Numbers

Selecting prime numbers at random is a requirement of many different key generation protocols. It is very time-consuming to check that a random number is truly a prime number, especially when dealing with numbers that have hundreds of digits.

The compromise between the need for prime numbers and the need to generate them in a reasonable time is to create numbers that are "probably" prime, which means that there is a small possibility that a number seems to be a prime number, but is actually not. Probable prime numbers are subject to a level of confidence, so that a level of 16 means that the probability that a number is a true prime number exceeds:

Some asymmetric encryption algorithms are significantly less secure if numbers that are supposed to be prime numbers turn out not to be, and so care must be taken when generating numbers with a low level of confidence. There is a balance between the confidence in a prime number and the amount of computation that is required to attain that confidence level.

15.1.2 Asymmetric Algorithm Security

Asymmetric algorithms use much longer keys than symmetric algorithms. In our examples, we selected small values to demonstrate the key generation protocol, but the numeric values used in practice contain many hundreds of digits.

Measure asymmetric key lengths in bits. The way to determine the number of bits differs between algorithms. The RSA algorithm specifies that the key length is the smallest number of bits needed to represent the value of the key modulus, n, using binary. Round up the number of bits to a factor of eight so that you can express the key using bytes; for example, consider a modulus represented by 509 bits to be a 512-bit key. Common lengths for keys are 512 and 1024-bits, but a 1024-bit asymmetric key does not provide 16 times more resistance to attack than a 64-bit symmetric key. Table 15-1 lists the equivalent asymmetric and symmetric key lengths accepted as providing equivalent resistance to brute force attacks (where Eve obtains the value of the private/secret key by testing all of the possible key values).

Most asymmetric algorithms rely on some form mathematical task that is difficult or time-consuming to perform. Cryptographers consider the RSA algorithm secure because it is hard to find the factors of a large number; given our example value for n (713), it would take some time to establish that the factors are the values you selected for p (23) and q (31). The longer the value of n, the longer it takes to determine the factors; bear in mind that the example value of n has only five digits, whereas the numbers that you would use for a secure key pair will be significantly longer.

Table 15-1. Asymmetric and symmetric key lengths providing equivalent resistance to brute force attacks
Symmetric key length	Asymmetric key length
64 bits	512 bits
80 bits	768 bits
112 bits	1792 bits
128 bits	2304 bits

Therefore, the essence of security for RSA is that given only the public key e and n, it takes a lot of computation to discover the private key d. Once you know the factors p and q, it is relatively easy to calculate d and decrypt ciphertext. Bob makes it difficult for Eve to decrypt his messages by keeping secret the values of d, p and q.

The main risk with asymmetric algorithms is that someone may discover a technique to solve the mathematical problems quickly, undermining the security of the algorithm. New techniques to factor large numbers might make it a simple process to decrypt messages or to deduce the value of the private key from the public key, and this would render the RSA algorithm (and any others that rely on the same mathematical problem) insecure.

15.1.3 Creating the Encrypted Data

We have already explained how the encryption and decryption functions are at the heart of an asymmetric algorithm, and the way in which we use these functions is similar to the techniques we discussed in Chapter 14. The protocol for encrypting data using an asymmetric algorithm is as follows:

Break the plaintext into small blocks of data.
Encrypt each small plaintext block by using the public key and the encryption function.
Concatenate the encrypted blocks to form the ciphertext.

The length of the public key determines the size of the block to which we break the plaintext. Each algorithm specifies a rule for working out how many bytes of data should be in each block, and for the RSA protocol, we subtract 1 from the key length (in bits) and divide the result by 8. The integral part of the result (the part of the number to the left of the decimal point) tells you how many bytes of data should be in each block of plaintext passed that is to the encryption function. You can work out how many bytes should be in a plaintext block for a 1024-bit key, as follows:

The integral value of the result is 127, meaning that when using the RSA algorithm with a 1024-bit public key we should break the plaintext into blocks of 127 bytes. The small key that you generated to demonstrate the key generation protocol is 16 bits long (713 is 1011001001 in binary and the bit length is therefore rounded up to be 16 bits) and with a 16-bit key, we must use 1-byte blocks (the integral part of (10 - 1)/8 = 1.875 is 1).

Encrypt each data block by interpreting it as an integer value and compute a ciphertext block using the RSA encryption function shown below (m is the integer value of the plaintext block and c is the ciphertext block):

c = m^e mod n

Figure 15-4 demonstrates how this process works for a 24-bit key, meaning that you process 2 bytes of plaintext at a time; the figure shows how the encryption function is applied to encrypt the string ".NET" into the ciphertext "35 7B AE 05 F1 6F."

Figure 15-4. Using the RSA encryption function to encrypt the string .NET using a 24-bit public key

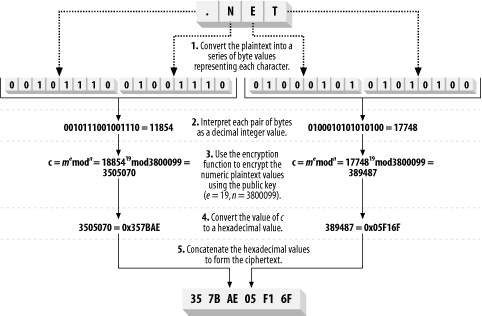
For reference, we created our 24-bit key using 1901 for p and 1999 for q. We chose e to be 19, giving a secret key value, d, of 2805887. Notice that the output of the cipher function is the same length as the key modulus, making the ciphertext larger than the plaintext.

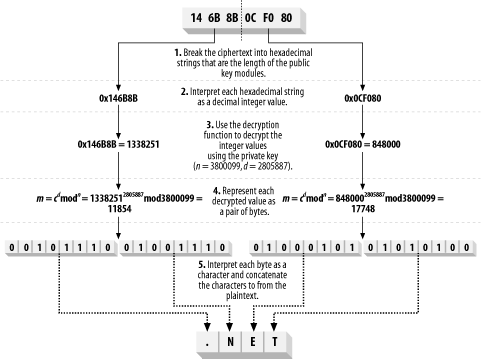
Decrypting data is the reverse of the encryption protocol:

Break the ciphertext into small blocks of data that are the same length as the public key modulus.
Decrypt each small ciphertext block by using the private key and the decryption function.
Concatenate the decrypted blocks to form the restored plaintext.

The decryption function is as follows (c is the value of the ciphertext block and m is the plaintext block):

m = c^d mod n

Notice that the decryption function uses the secret key (d) and the modulus from the public key (n). Figure 15-5 demonstrates how this process works for our 24-bit key, meaning that we process 3 bytes of ciphertext at a time; the figure shows how we decrypt the ciphertext that we created in Figure 15-4.

Figure 15-5. Using the RSA decryption function

15.1.3.1 Asymmetric data padding

Asymmetric encryption algorithms rely on padding to protect against specific kinds of attack, in much the same way that symmetric algorithms rely on cipher feedback. Padding schemes also ensure that the encryption function does not have to process partial blocks of data.

Asymmetric padding schemes are a series of instructions that specify how to prepare data before encryption, and usually mix the plaintext with other data to create a ciphertext that is much larger than the original message. The .NET Framework supports two padding schemes for the RSA algorithm: Optimal Asymmetric Encryption Padding (OAEP) and PKCS #1 v1.5. OAEP is a newer scheme that provides protection from attacks to which the PKCS #1 v1.5 scheme is susceptible. You should always use OAEP, unless you need to exchange encrypted data with a legacy application that expects PKCS #1 v1.5 padding.

We do not discuss the details of either padding scheme in this book; it is important only that you understand that padding is used in conjunction with the asymmetric algorithm to further protect confidential data.