14.2 Symmetric Encryption Explained
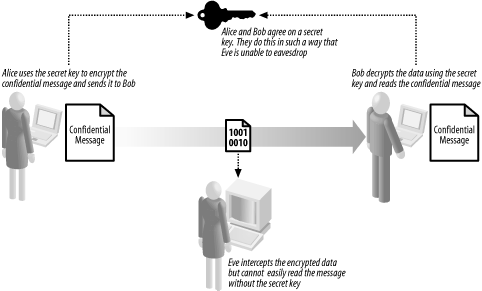
Symmetric encryption is the oldest and most established way of ensuring message confidentiality, dating back for many thousands of years. Figure 14-2 illustrates the basic approach, which is as follows:
Alice and Bob agree on a secret key.
Alice composes a confidential message to Bob and encrypts it using the secret key.
Alice sends the encrypted data to Bob.
Bob uses the secret key to decrypt the encrypted data, and reads the confidential message.
The most important aspect of symmetric encryption is that Alice and Bob agree on a secret key without Eve eavesdropping. If Eve acquires the secret key, she will be able to read, modify. and forge messages between Alice and Bob. The traditional means of agreeing on secret key has been to meet in person at a private location, or to rely on a secure and trusted courier service, both of which can be difficult to arrange securely.
Figure 14-2. Alice and Bob use symmetric encryption to ensure message confidentiality
14.2.1 Creating the Encrypted Data
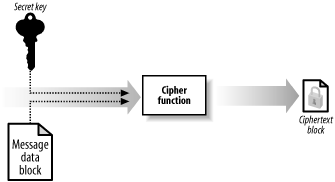
At the heart of a symmetric encryption algorithm is a cipher function that transforms fixed-size blocks of message data, known as plaintext, into blocks of encrypted data, known as ciphertext, illustrated by Figure 14-3. This type of function is a block cipher, because it processes blocks of data sequentially and independently. The output of a block ciphers is deterministic; this means that a given block of plaintext encrypted using a given key will always result in the same block of ciphertext. Different block ciphers process differently sized blocks of plaintext.
Figure 14-3. A cipher function uses a secret key and a fixed-size message block to create a block of ciphertext
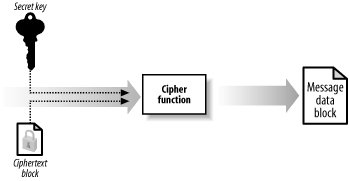
You can restore a block of plaintext from a block of ciphertext by reversing the transformation, as illustrated by Figure 14-4. Both the transformation into ciphertext and the restoration of the plaintext require the secret key; therefore, Bob can decrypt the data only if he uses the same secret key that Alice used to encrypt the message. This is different from the hash functions we examined in Chapter 13; encryption is a reversible, or "two-way," process, where we can use the secret key to "reverse" the encryption effect and restore the plaintext. Creating a hash code is a "one-way" process, and the original message data cannot be determined from the hash code data easily.
Figure 14-4. Cipher functions also transform ciphertext back into plaintext, which is known as decryption
An encryption algorithm is the protocol for using a cipher function to encrypt plaintext, in the same way that a hashing algorithm specifies how to use a hash function to create a hash code. The algorithm specifies how the plaintext is broken into blocks and how to use the output of the cipher function in creating the ciphertext; the details of how to perform these tasks differ between algorithms.
On a practical basis, the .NET Framework provides a standardized model for using symmetric encryption algorithms, and you do not have to understand the inner workings of any specific block ciphers. However, you should understand some of the different ways that you can configure an algorithm, which we discuss in the following sections.
14.2.2 Cipher Modes
Most symmetric encryption algorithms operate in different cipher modes, which specify variations in the way that data is prepared before being processed by the cipher function. The following sections explain the most commonly used modes, but you should bear in mind that there are a large number of variations and not all algorithms can support all cipher modes.
14.2.2.1 Electronic Codebook mode
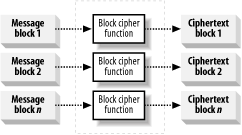
The Electronic Codebook (ECB) mode is the simplest cipher mode and builds ciphertext by concatenating the output of the cipher function, as shown in Figure 14-5. We can summarize the process as follows:
Break the plaintext into blocks that are the same size as the input of the cipher function.
Use the secret key to encrypt each plaintext data block in turn with the cipher function.
Append the output of the cipher function to the ciphertext.
Figure 14-5. The ECB mode is the simplest way to encrypt data with a block cipher function
Although this seems like the obvious way to encrypt data, the deterministic nature of the cipher function exposes the ciphertext to a special kind of attack whenever there is repetition in the confidential message.
The cipher function is consistent, and using a secret key to encrypt two identical blocks of data results in identical blocks of ciphertext. If there are any repeated blocks of data in the plaintext, you will end up with repeated blocks of data in the ciphertext, which presents a weakness that Eve can exploit.
There is a natural structure to many types of messages; for example, Alice's letters often begin with "Dear Bob" and emails will often start with "From," "To," or "Received." Imagine that Alice sends a company memo to Bob, and that Eve knows (or can guess at) the structure of such messages.
Figure 14-6 shows a simplified representation of the effect of building the ciphertext from the output of the cipher function directlysimplified because we have assumed that each word is encrypted as a plaintext block in a case-insensitive manner. Real encryption algorithms work on binary data, but our example is useful for understanding the issue at hand. Eve knows that all of Alice's memos begin with "From," and therefore knows that the first block of ciphertext represents that word. Eve knows that every time she finds that particular ciphertext block in the encrypted data she has located another instance of the word "From." By applying her knowledge of the message structure, Eve deduces several words in the confidential message, including the words "To," "Bob," "Subject," and "Alice."
Figure 14-6. Eve uses plaintext repetition to build a codebook of known ciphertext blocks

Eve finds repeated ciphertext blocks for which she can't deduce the meaning, because the word that the block represents is not included in the standard structure of Alice's memo; AAA and BBBB indicate these blocks. Regardless, Eve keeps a record of these blocks, because she may intercept another message that reveals their meaning later and shed more light on this messagea process of building a codebook that will help her recognize the meaning of known ciphertext blocks as she intercepts them. Eve's "codebook" is useful only while Alice and Bob use the same secret key. If they agree on a new key, the ciphertext blocks for known words will be different, and Eve will have to start from scratch.
The ECB mode is the simplest way to create ciphertext, although the risks associated with encrypting duplicate plaintext blocks mean that you should use it with caution. The following sections describe alternate cipher modes that address the problem of block repetition, and we recommend that you use these instead of ECB.
14.2.2.2 Cipher block chaining
The most common way to overcome the block repetition weakness of ECB is to add "feedback" into the cipher function. Adding feedback produces a ciphertext in which the result of encrypting a data block affects the results of encrypting all subsequent blocks. Figure 14-7 illustrates the most widely used way of doing this, called Cipher Block Chaining (CBC), which works as follows:
Break the plaintext into blocks that are the same size as the input for the cipher function.
Process the first message block:
XOR the message block with the "seed" data to create a combined data block.
Encrypt the result to produce the first block of ciphertext.
Process remaining message blocks in turn:
XOR the plaintext block with most recently created ciphertext block to create a combined data block.
Encrypt the combined data block and append the result to the ciphertext.
Figure 14-7. CBC uses the result of previous encryptions to transform plain text blocks
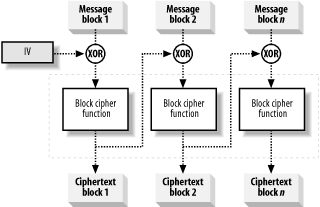
For example, to encrypt the 10th plaintext block you XOR it with the 9th ciphertext block and encrypt the result, producing the 10th ciphertext block, which you XOR with the 11th plaintext block, and so on.
The seed data for symmetric encryption is called the initialization vector (IV) and is used to ensure that the first block of ciphertext is not open to ECB-style attacks. The IV is a block of random data that is the same size as the cipher function input block.
Using CBC means that Bob has to use the same IV to decrypt the data as Alice used to encrypt the message; fortunately, the value of the IV is not a secret, and there is no danger in allowing it to fall into Eve's hands. Alice should select a new IV for each message that she encrypts, and she will normally send the IV to the recipient along with the encrypted data.
14.2.2.3 Cipher feedback mode
Processing plaintext data block by block is not suitable for all projects, especially those where the data to encrypt becomes available over time (for example, received via a network stream). In such cases, the confidential data has to be held in memory until a complete block is received and encrypted, which can present a security risk.
Cipher Feedback (CFB) mode is a technique for using a block cipher function to encrypt plaintext in fragments smaller than the function block size, allowing data to be encrypted as it arrives. Like CBC, CFB uses an IV, but in this mode, it represents the initial value for a queue, which is a data block the same size as the cipher function input. If you are using a cipher that operates on 64-bit data blocks but the data becomes available in 8-bit chunks, then the CFB protocol is as follows:
Create a 64-bit queue, and fill it with a 64-bit IV.
As each 8-bit chunk of plaintext becomes available:
Encrypt the queue.
XOR the leftmost eight bits of the encrypted queue with the eight bits of plaintext to create the cipher data chunk.
Append the cipher data chunk to the ciphertext output.
Shift the queue eight bits to the left and discard the leftmost eight bits.
Set the rightmost eight bits of the queue to be the eight bits of ciphertext.
This seems a lot more complicated than it actually is. Start with a 64-bit queue that contains the IV, and as you progress, the queue gradually fills up with 8-bit chunks of ciphertext. Figure 14-8 illustrates the way in which CFB works.
Figure 14-8. CFB mode uses a queue to process small chunks of data
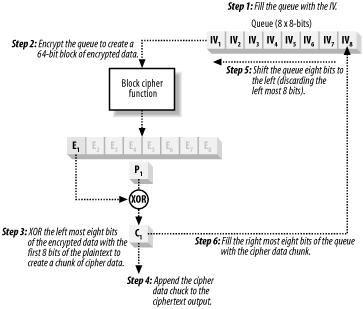
CFB encrypts data one bit at a time if required, although that would use a lot of CPU (because the cipher function encrypts a complete block of data for each message bit). In the queue, the gradual shifting of the data protects against ECB attacks.
14.2.3 Block Padding
Most messages do not divide neatly into the fixed-size blocks required by the cipher function, and there is usually a partial data block left over at the end. The cipher function cannot process partial blocks, and the algorithm adds "padding" to the leftover data to create a complete block.
Padding, unlike other aspects of encryption, is expressed in bytes rather than bits. For example, if you are using a cipher that processes 64-bit blocks, a 13-byte (104-bit) message breaks down into one complete data block with 40 bits remaining. We need to add 3 bytes (24 bits) of data to the remainder to create a second block that the cipher function can process. There are two commonly used approaches to block padding, and the .NET Framework supports both. The first approach is simply to set the remaining bytes to 0, as shown in Figure 14-9.
Figure 14-9. Using zeros to pad a partial data block
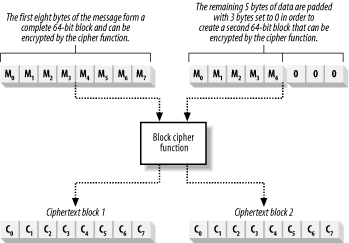
Encrypt the padded plaintext block, and the result is appended to the ciphertext; note that the ciphertext will be three bytes larger than the plaintext. When you decrypt the ciphertext, remove the padding values to return to the original plaintext message. The problem with this approach is that it is difficult to be sure that you are removing the padding correctly; some algorithms naturally generate strings of zeros, and you may remove bytes that are part of the message.
A more reliable approach is to use PKCS #7 padding, where you set the value of the padding bytes to the number of bytes you added. For our example, the padding would be three bytes set to a value of "3". When you remove the padding, simply read the value of the last byte and you can tell which bytes you have to remove, as shown in Figure 14-10.
Figure 14-10. Using PKCS #7 padding to complete a partial data block
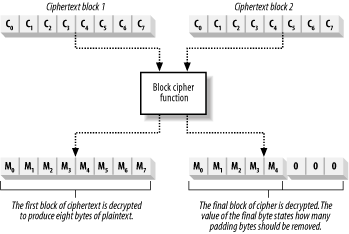
You still have to add PKCS #7 padding even when there are no partial plaintext blocks to process. This is because many algorithm implementations examine the numeric value of the last byte, and do not check to ensure that all of the padding bytes are set to the same value. When the plaintext results in only whole blocks, add a complete block of padding data, with all of the byte values set to be 1/8th of the block size; for a 64-bit block cipher, this would be 8 bytes of value "8". When the ciphertext is decrypted, remove the entire final block to leave the original plaintext. PKCS #7 padding is limited to 256 bytes of padding, which is the largest numeric value a single byte of data can represent.
14.2.4 Symmetric Encryption Key Lengths
The security of symmetric encryption comes from the fact that Eve does not have the secret key. If she did, she would be able to read any of Alice's messages to Bob and even forge new messages by using the secret key to encrypt them.
We describe secret keys by their length, measured in bits. A 64-bit key can represent 264 different key values, and a 256-bit key can represent 2256 different key values. Symmetric encryption keys are typically attacked using brute force, where Eve tries all of the possible keys until she finds the one that Alice and Bob have selected. Protect the confidential messages by making it hard for Eve to try all of the possible keys; the longer you make the key, the longer it takes Eve to check all of the possible key values.
Probability and Brute Force AttacksWhen you see calculations that tell you how long it takes to guess a secret key, you should be aware of two assumptions that are rarely stated:
If you consider these assumptions, you will notice that there is a fundamental conflict. For a randomly selected key, Eve may be lucky and find that the first key that she checks is the one that she is looking for. It will take Eve 11.6 billion years to try all the possible values for a 64-bit key if she can test 50 keys per second, but there is a 50% chance that she will find a match after checking only half the key space and a 1 in 264 chance that the first key she checks will be the one that Alice and Bob have used. When assessing the security of keys, always bear in mind that brute force attacks are subject to the laws of probability, and it's a very optimistic expectation to hope that Eve will have to check all possible keys. If Eve knows that the key is contained in a specific range, then the situation is even worse: not only is early success still possible but she is also able to reduce the total number of keys to check. See Chapter 17 for more information about selecting and managing keys. |
Assess the length of the key you need by estimating how many candidate keys Eve can test per second then compare this with how long you need to maintain confidentiality. For example, if Eve could check 50 candidate keys per second, it would take her 11.6 billion years to check all of the possible values for a 64-bit key. Symmetric cryptography is not subject to the birthday attacks we mentioned in Chapter 13, and calculating the relative security of a key is a simple process. If Eve checks more keys per second, then you will have to adjust your projections accordingly.
The trade-off is that encrypting and decrypting data using longer keys requires more computation, and using very long keys is practical only when you are using high-end computers. Make a reasonable estimate of your confidentiality requirements when selecting a key length and include an estimation of how Eve's ability to perform brute force attacks will change over time. History shows us that improvements in design and manufacturing halve the cost of processing power every 18 months; therefore, over time Eve will be able to increase her ability to check candidate keys for each dollar that she spends.
14.2.5 The .NET Framework Encryption Algorithms
The .NET Framework provides classes for four different symmetric encryptions. Table 14-1 summarizes the encryption algorithms available and the possible secret key lengths.
|
Name |
Block size |
Key length (bits) |
|---|---|---|
|
DES |
64 |
56 (although conventionally expressed as a 64-bit number) |
|
RC2 |
64 |
40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128 |
|
Triple-DES |
64 |
Two or three 56-bit keys, expressed as 64-bit numbers |
|
Rijndael (AES) |
128, 192, 256 |
128, 192, 256 |
Based on the Lucifer cipher developed by IBM, the Data Encryption Standard (DES) algorithm was published in 1976 and has been used in a huge range of applications. The design has aged remarkably well, given it's rocky beginnings. To produce DES, the National Security Agency modified the Lucifer cipher in a way that was thought to compromise security. (A common theory throughout recent cryptographic history is that the National Security Agency is tinkering behind the scenes to limit the efficacy of cryptography.) The limit of a 56-bit key means that DES is becoming increasingly susceptible to exhaustive key searches using modern computers, but various efforts have been made to prolong the life of this venerable cipher, most notably the Triple-DES standard. The Advanced Encryption Standard (AES) officially succeeded DES in 2001 as the principal U.S. federal standard for data encryption.
The RC2 algorithm was developed by Ron Rivest of RSA (also responsible for the MD5 hashing algorithm discussed in Chapter 13) as a direct replacement for DES. Controversy dogged the acceptance of RC2, because RSA decided to keep the details of the cipher secret, preventing proper security analysis. In 1997, RSA published the details of the algorithm to foster the adoption of the S/MIME standard, which acts as a framework for cryptographically secure email. A wide range of products use RC2, and it has become one of the most commonly used symmetrical ciphers. RC2 operates with key lengths ranging from 40 to 128 bits.
Designed to prolong the life of DES, Triple-DES encrypts data three times using the DES algorithm. A different 56-bit key can be used for each encryption step, or two 56-bit keys can be used and the third encryption step will be performed using the first key. Triple-DES has found a lasting niche in the international financial markets for encrypting banking data.
Rijndael (pronounced "RAIN-Dahl" or "REIN-Daal") was the winner of the U.S. Government's selection process for the AES, which is the successor to the aging DES algorithm. Unlike the other algorithms included in the .NET Framework, the Rijndael cipher function operates on a range of data block sizes. Although tested rigorously during selection, cryptographers have not yet established the long-term security of the Rijndael/AES algorithm. You should exercise caution before using Rijndael, and remember that it takes a great deal of time and analysis before a new algorithm can be fully trusted.







