15.3 Extending the .NET Framework
In this section, we demonstrate how to extend the .NET Framework by adding a new asymmetric encryption algorithm. We have selected the ElGamal algorithm, and we will implement the base classes and the core encryption functions. In the following chapters, we will extend our implementation to include support for digital signatures and padding schemes.
We have provided only a C# implementation of the ElGamal algorithm. Like almost all encryption algorithms, ElGamal relies on mathematical operations that are not possible in Visual Basic .NET without creating additional support functions to compensate for the limited numeric support the language provides.
15.3.1 The ElGamal Algorithm Explained
Taher ElGamal published the ElGamal algorithm in 1985, and it has been widely adopted as an alternative to RSA, where licensing and patents have been an issue (the RSA algorithm was protected by a patent that has now expired, whereas no patents were obtained for ElGamal).
ElGamal relies on a different mathematical problem than the factoring of large numbers used by the RSA algorithm; this problem is finding the discrete logarithm of a large integer value. The ElGamal algorithm is as secure as RSA, but encrypts data slower; the algorithm is the basis for the Digital Signature Algorithm, which we discuss in the following chapter.
15.3.1.1 ElGamal key generation protocol
The key generation protocol for the ElGamal algorithm is as follows; we will select small values to demonstrate the key generation, and then use this key to show how the encryption and decryption functions operate:
Create a random prime number, p. This number is the ElGamal "modulus." The number of bits required to represent p is the size of the public key, so that if p is represented using 1024 bits, then the key created by following the protocol is a 1024-bit key. We will select 607 as our example value.
Select two other random numbers, g and x, both of which are less than p; these numbers do not have to be prime. We will select 23 as our value of g, and 152 as our value of x.
Compute y, where y = gxmodp
For our example, we calculate y as follows:
y = 23152mod607 = 209
The public key is p, g and y. The private key is x.
15.3.1.2 ElGamal encryption and decryption functions
The ElGamal algorithm encrypts only numeric values that are less than the modulus, p. In order to encrypt messages greater than the modulus, we must break the plaintext into smaller values, just as we did with the RSA algorithm.
The ElGamal encryption function is as follows:
Break the plaintext into blocks based on the length of the public key modulus.
Process each plaintext block, m:
Choose a random number, k, relatively prime to p - 1 (i.e., k and p - 1 have no common factors).
Compute a = gkmodp
Compute b = (ykm)modp
Concatenate a and b to form an encrypted data block.
Concatenate the encrypted data blocks to form the ciphertext.
The size of the ciphertext created by the encryption function is double the size of the plaintext; this is not an issue for most projects because asymmetric algorithms are typically used to encrypt only small amounts of data; see Chapter 17 for more details.
The ElGamal decryption function is as follows:
Break the ciphertext into blocks that are twice the length of the key modulus.
Process each ciphertext block:
Break the ciphertext block in half to form a and b.
Use the private key to compute the decrypted block m where
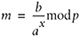
Concatenate the decrypted blocks to form the plaintext.
These functions are the "raw" algorithm; like RSA, ElGamal is always used in conjunction with a padding scheme, usually OAEP. In this chapter, we implement the raw algorithm, setting the padding aside until Chapter 17.
15.3.2 Processing Large Integer Values
One problem that asymmetric algorithms present is the need to perform arithmetic operations on very large integer values, often containing many hundreds of digits. The .NET Framework cannot process numbers that require more than 64 bits to represent, falling short of our requirements, where 1024- and 2048-bit numbers are commonly required.
Our ElGamal implementation relies on the BigInteger class written and placed in the public domain[1] by Chew Keong Tan. The BigInteger class represents large integer values by using arrays of 32-bit integers and includes useful methods for many mathematical functions, including the generation of probable prime numbers.
[1] The following statements comprise the copyright declaration and the license for Chew Keong Tan's BigInteger class:
We have included the BigInteger class in the ElGamal example code, and with the exception of one small change, we use the same version that you can download from the internet. The change we have made is to double the largest value that the class can represent by increasing the maxLength variable to 140. You do not have to be concerned with the details of this change or the implementation of the class. Table 15-6 describes the class members that we use for our algorithm implementation.
|
Member |
Description |
|---|---|
|
Constructors | |
|
BigInteger(byte[]) |
Creates a new instance from an array of signed byte values |
|
BigInteger(long) BigInteger(int) |
Creates a new instance representing the numeric value specified by the long or int argument |
|
BigInteger(BigInteger) |
Creates a new instance with the same value as the argument |
|
Methods | |
|
modPow(BigInteger exp, BigInteger m) |
Returns the value (thisexp mod m) |
|
modInverse(BigInteger m) |
Returns the value (this-1mod m) |
|
getBytes( ) |
Converts the integer into a series of signed byte values |
|
bitCount( ) |
Calculates how many bits are required to express the integer value |
|
genPseudoPrime(int bits, int confidence, Random rand) |
Generates a random positive BigInteger with the specified number of bits and confidence level, using the provided random number generator |
|
genRandomBits(int bits, Random rand) |
Creates a random number with the specified number of bits, using the provided random number generator |
15.3.3 Defining the Abstract Class
We start by defining the ElGamalParameters structure, which we use to import and export keys to and from the implementation classes without exposing our dependence on the BigInteger class; this is equivalent to the RSAParameters structure used by the RSA implementation classes:
[Serializable]
public struct ElGamalParameters {
public byte[] P;
public byte[] G;
public byte[] Y;
[NonSerialized] public byte[] X;
}
We have annotated the structure with the Serializable attribute so that users of the ElGamal implementation can store public keys persistently, but we have used the NonSerialized attribute to ensure that the private key cannot be persisted. We express the value of P, G, Y and X as byte arrays for consistency with the rest of the .NET Framework, even though we will represent these values internally using the BigInteger class:
public abstract class ElGamal : AsymmetricAlgorithm {
public abstract void ImportParameters(ElGamalParameters p_parameters);
public abstract ElGamalParameters ExportParameters(bool
p_include_private_params);
We have called our abstract class ElGamal, in keeping with the standard naming model. The ImportParameters and ExportParameters methods set and get the state of the algorithm using instances of the ElGamalParameters structure we defined previously:
public abstract byte[] EncryptData(byte[] p_data);
public abstract byte[] DecryptData(byte[] p_data);
public abstract byte[] Sign(byte[] p_hashcode);
public abstract bool VerifySignature(byte[] p_hashcode, byte[] p_signature);
The remaining abstract methods define the asymmetric encryption and digital signature functions we support; for simplicity we will not support padding schemes in the algorithm class, which allows us to define an abstract class that can be used directly (unlike the RSA implementation, where the methods defined by the abstract class are not implemented by the Crypto API implementation).
The only methods that are not abstract are ToXmlString and FromXmlString, required by the AsymmetricAlgorithm class. We can implement these in the abstract class safely because the implementation gets and sets the details about the key using the abstract ImportParameters and ExportParameters methods; the implementation details do not affect the way in which the XML string is processed:
public override string ToXmlString(bool p_include_private) {
ElGamalParameters x_params = ExportParameters(p_include_private);
// create a new string builder
StringBuilder x_sb = new StringBuilder( );
// add the header
x_sb.Append("<ElGamalKeyValue>");
// add the public elements from the parameters
x_sb.Append("<P>" + Convert.ToBase64String(x_params.P) + "</P>");
x_sb.Append("<G>" + Convert.ToBase64String(x_params.G) + "</G>");
x_sb.Append("<Y>" + Convert.ToBase64String(x_params.Y) + "</Y>");
if (p_include_private) {
// we need to include X, which is the part of private key
x_sb.Append("<X>" + Convert.ToBase64String(x_params.X) + "</X>");
}
// add the final element
x_sb.Append("</ElGamalKeyValue>");
return x_sb.ToString( );
}
public override void FromXmlString(String p_string) {
// create the params that we will use as the result
ElGamalParameters x_params = new ElGamalParameters( );
// create a text reader using a string reader
XmlTextReader x_reader =
new XmlTextReader(new System.IO.StringReader(p_string));
// run through the elements in the xml string
while (x_reader.Read( )) {
// we are only interested in processing start nodes
if (true || x_reader.IsStartElement( )) {
switch (x_reader.Name) {
case "P":
// set the value for P
x_params.P =
Convert.FromBase64String(x_reader.ReadString( ));
break;
case "G":
// set the value for G
x_params.G =
Convert.FromBase64String(x_reader.ReadString( ));
break;
case "Y":
// set the value for Y
x_params.Y =
Convert.FromBase64String(x_reader.ReadString( ));
break;
case "X":
// set the value for X (this would not be found in a
// string that was generated by excluding the private
// elements.
x_params.X =
Convert.FromBase64String(x_reader.ReadString( ));
break;
}
}
}
// Import the result
ImportParameters(x_params);
}
}
15.3.4 Defining the Implementation Class
Begin the implementation by defining a structure that you can use privately to represent the key as a series of BigIntegers. The ElGamalKeyStruct structure makes processing blocks of data simpler, because you do not need to convert the byte arrays represented by the ElGamalParameters to integer values each time you need to use one of the key parameters:
using System;
using System.Security.Cryptography;
public struct ElGamalKeyStruct {
public BigInteger P;
public BigInteger G;
public BigInteger Y;
public BigInteger X;
}
The name of our implementation class is ElGamalManaged, in keeping with the .NET cryptographic naming model. This class extends the ElGamal abstract algorithm class, and defines an ElGamalKeyStruct instance variable that you use to represent the current key in use:
public class ElGamalManaged : ElGamal {
private ElGamalKeyStruct o_key_struct;
The first part of the constructor initializes the BigIntegers contained in the ElGamalKeyStruct to 0; this gives a known starting point, and you can assume the user has not imported a key if the public key parameter values are all set to 0:
public ElGamalManaged( ) {
// create the key struct
o_key_struct = new ElGamalKeyStruct( );
// set all of the big integers to zero
o_key_struct.P = new BigInteger(0);
o_key_struct.G = new BigInteger(0);
o_key_struct.Y = new BigInteger(0);
o_key_struct.X = new BigInteger(0);
The other task the constructor performs defines the range of key lengths that the implementation supports. We have selected 384 bits as the shortest key supported to conform to the .NET RSA implementation. We define 1088 bits as the largest value because of the size limitations when using the BigInteger class; even though we have doubled the largest value that this class can represent, we still exceed that limit when performing the encryption computation for larger key sizes. We set the default key size to be 1024 bits, which provides a key strength that is suitable for most projects:
// set the default key size value
KeySizeValue = 1024;
// set the range of legal keys
LegalKeySizesValue = new KeySizes[] {new KeySizes(384, 1088, 8)};
}
The SignatureAlgorithm and KeyExchangeAlgorithm properties return a string value that indicates how the class performs encryption and creates digital signatures; we are implementing the "raw" ElGamal algorithm, and so both of these properties simply return ElGamal:
public override string SignatureAlgorithm {
get {
return "ElGamal";
}
}
public override string KeyExchangeAlgorithm {
get {
return "ElGamal";
}
}
The CreateKeyPair method follows the ElGamal key generation protocol to create a new key pair; the key parameter values are set using the ElGamalKeyStruct instance variable; the method accepts an integer argument that specifies the required key length:
private void CreateKeyPair(int p_key_strength) {
// create the random number generator
Random x_random_generator = new Random( );
// create the large prime number, P
o_key_struct.P = BigInteger.genPseudoPrime(p_key_strength,
16, x_random_generator);
// create the two random numbers, which are smaller than P
o_key_struct.X = new BigInteger( );
o_key_struct.X.genRandomBits(p_key_strength -1, x_random_generator);
o_key_struct.G = new BigInteger( );
o_key_struct.G.genRandomBits(p_key_strength -1, x_random_generator);
// compute Y
o_key_struct.Y = o_key_struct.G.modPow(o_key_struct.X, o_key_struct.P);
}
}
The NeedToGenerateKey method tests the value of the public key parameters; if all of the values are 0, then we assume that the user has not imported a key and that we should create a new key pair before encrypting or decrypting data. The KeyStruct property simply gets or sets the ElGamalKeyStruct instance member:
private bool NeedToGenerateKey( ) {
return o_key_struct.P == 0 && o_key_struct.G == 0 && o_key_struct.Y == 0;
}
public ElGamalKeyStruct KeyStruct {
get {
if (NeedToGenerateKey( )) {
CreateKeyPair(KeySizeValue);
}
return o_key_struct;
}
set {
o_key_struct = value;
}
}
The ImportParameters method accepts an instance of the ElGamalParameters structure and creates the BigIntegers that we will use to represent the key; this method allows users to import a previously created key and is used by the FromXmlString method in the abstract ElGamal class:
public override void ImportParameters(ElGamalParameters p_parameters) {
// obtain the big integer values from the byte parameter values
o_key_struct.P = new BigInteger(p_parameters.P);
o_key_struct.G = new BigInteger(p_parameters.G);
o_key_struct.Y = new BigInteger(p_parameters.Y);
if (p_parameters.X != null && p_parameters.X.Length > 0) {
o_key_struct.X = new BigInteger(p_parameters.X);
}
// set the length of the key based on the import
KeySizeValue = o_key_struct.P.bitCount( );
}
The ExportParameters method creates an ElGamalParameters structure using the key represented by the instance ElGamalKeyStruct member. Notice that we check to see if we need to create a new key pair before we export the key details to ensure that there is something to export. The Boolean argument determines whether to export the private parameters, in keeping with the model used by the RSA implementation classes:
public override ElGamalParameters ExportParameters(bool
p_include_private_params) {
if (NeedToGenerateKey( )) {
// we need to create a new key before we can export
CreateKeyPair(KeySizeValue);
}
// create the parameter set
ElGamalParameters x_params = new ElGamalParameters( );
// set the public values of the parameters
x_params.P = o_key_struct.P.getBytes( );
x_params.G = o_key_struct.G.getBytes( );
x_params.Y = o_key_struct.Y.getBytes( );
// if required, include the private value, X
if (p_include_private_params) {
x_params.X = o_key_struct.X.getBytes( );
} else {
// ensure that we zero the value
x_params.X = new byte[1];
}
// return the parameter set
return x_params;
}
The EncryptData and DecryptData methods provide access to the ElGamal encryption and decryption functions; create a new key pair if the user has not imported a key, and then pass the data to the specialized ElGamalEncryptor and ElGamalDecryptor classes, which we detail in the next sections:
public override byte[] EncryptData(byte[] p_data) {
if (NeedToGenerateKey( )) {
// we need to create a new key before we can export
CreateKeyPair(KeySizeValue);
}
// encrypt the data
ElGamalEncryptor x_enc = new ElGamalEncryptor(o_key_struct);
return x_enc.ProcessData(p_data);
}
public override byte[] DecryptData(byte[] p_data) {
if (NeedToGenerateKey( )) {
// we need to create a new key before we can export
CreateKeyPair(KeySizeValue);
}
// encrypt the data
ElGamalDecryptor x_enc = new ElGamalDecryptor(o_key_struct);
return x_enc.ProcessData(p_data);
}
The Dispose method is useful for releasing unmanaged resources, but you do not need to do anything in this method since the implementation is written entirely in managed code, but it is a requirement of extending from the AsymmetricAlgorithm class:
protected override void Dispose(bool p_bool) {
// do nothing - no unmanaged resources to release
}
The Sign and VerifySignature methods support the creation and verification of digital signatures; although you have implemented these methods to comply with the abstractions of the ElGamal class, we will not explain their use, or detail the classes they call until Chapter 16:
public override byte[] Sign(byte[] p_hashcode) {
throw new System.NotImplementedException( );
}
public override bool VerifySignature(byte[] p_hashcode, byte[] p_signature) {
throw new System.NotImplementedException( );
}
15.3.5 Defining the Abstract Cipher Function Class
We use the ElGamalAbstractCipher class as the basis for the encryption and decryption classes; it contains methods that are common to both functions. This class is also responsible for breaking up an array of data into blocks that can be processed using the current public key (remember that the length of the key modulus affects the amount of data that can be processed by the encryption function in one go):
using System;
using System.IO;
public abstract class ElGamalAbstractCipher {
protected int o_block_size;
protected int o_plaintext_blocksize;
protected int o_ciphertext_blocksize;
protected ElGamalKeyStruct o_key_struct;
public ElGamalAbstractCipher(ElGamalKeyStruct p_key_struct) {
// set the key details
o_key_struct = p_key_struct;
// calculate the blocksizes
o_plaintext_blocksize = (p_key_struct.P.bitCount( ) -1) / 8;
o_ciphertext_blocksize = ((p_key_struct.P.bitCount( ) + 7) / 8) * 2;
// set the default block for plaintext, which is suitable for encryption
o_block_size = o_plaintext_blocksize;
}
The constructor accepts an ElGamalKeyStruct structure as an argument, which is used to work out the size of the blocks that will be used by the encryption and decryption functionsthe ElGamal encryption function produces ciphertext that is twice the size of the corresponding plaintext:
public byte[] ProcessData(byte[] p_data) {
// create a stream backed by a memory array
MemoryStream x_stream = new MemoryStream( );
// determine how many complete blocks there are
int x_complete_blocks = p_data.Length / o_block_size;
// create an array which will hold a block
byte[] x_block = new Byte[o_block_size];
// run through and process the complete blocks
int i = 0;
for (; i < x_complete_blocks; i++) {
// copy the block and create the big integer
Array.Copy(p_data, i * o_block_size, x_block, 0, o_block_size);
// process the block
byte[] x_result = ProcessDataBlock(x_block);
// write the processed data into the stream
x_stream.Write(x_result, 0, x_result.Length);
}
// process the final block
byte[] x_final_block = new Byte[p_data.Length -
(x_complete_blocks * o_block_size)];
Array.Copy(p_data, i * o_block_size, x_final_block, 0,
x_final_block.Length);
// process the final block
byte[] x_final_result = ProcessFinalDataBlock(x_final_block);
// write the final data bytes into the stream
x_stream.Write(x_final_result, 0, x_final_result.Length);
// return the contents of the stream as a byte array
return x_stream.ToArray( );
}
The ProcessData method uses the block sizes calculated in the constructor to process an array of data; the array is broken down into data blocks and passed to the ProcessDataBlock and ProcessFinalDataBlock using the model laid down by the ICryptoTransform interface you saw in Chapter 14.
The ProcessDataBlock and ProcessFinalDataBlock methods are abstract, and the encryption and decryption subclasses must implement them in order to process the blocks of data created by the ProcessData method:
protected abstract byte[] ProcessDataBlock(byte[] p_block);
protected abstract byte[] ProcessFinalDataBlock(byte[] p_final_block);
}
15.3.6 Defining the Encryption Class
The ElGamalEncryptor class extends ElGamalAbstractCipher and is responsible for producing ciphertext using the ElGamal encryption cipher; the EncryptData method in the ElGamalManaged class uses this class:
using System;
public class ElGamalEncryptor : ElGamalAbstractCipher {
Random o_random;
public ElGamalEncryptor(ElGamalKeyStruct p_struct) : base(p_struct) {
o_random = new Random( );
}
The constructor creates a new random number generator, which the BigInteger class uses to create the large random value K, required by the encryption function. The ProcessDataBlock method represents the encryption function, and computes the A and B values that we discussed in the introduction to the ElGamal algorithm; these values are concatenated to form a single ciphertext block that is the method return value:
protected override byte[] ProcessDataBlock(byte[] p_block) {
// the random number, K
BigInteger K;
// create K, which is the random number
do {
K = new BigInteger( );
K.genRandomBits(o_key_struct.P.bitCount( ) -1, o_random);
} while (K.gcd(o_key_struct.P -1) != 1);
// compute the values A and B
BigInteger A = o_key_struct.G.modPow(K, o_key_struct.P);
BigInteger B = (o_key_struct.Y.modPow(K, o_key_struct.P)
* new BigInteger(p_block)) % (o_key_struct.P);
// create an array to contain the ciphertext
byte[] x_result = new byte[o_ciphertext_blocksize];
// copy the bytes from A and B into the result array
byte[] x_a_bytes = A.getBytes( );
Array.Copy(x_a_bytes, 0, x_result, o_ciphertext_blocksize / 2
- x_a_bytes.Length, x_a_bytes.Length);
byte[] x_b_bytes = B.getBytes( );
Array.Copy(x_b_bytes, 0, x_result, o_ciphertext_blocksize
- x_b_bytes.Length, x_b_bytes.Length);
// return the result array
return x_result;
}
The ElGamalAbstractCipher class calls the ProcessFinalDataBlock method to encrypt the last block of plaintext, which may not be a complete block; the block is padded with 0 as required, and then passed to the ProcessDataBlock method for encryption. If the data block contains no data, then assume that the plaintext is divided into blocks with no partial data remaining, and therefore there is no remaining data for encryption. In this case, simply return an empty byte array:
protected override byte[] ProcessFinalDataBlock(byte[] p_final_block) {
if (p_final_block.Length > 0) {
if (p_final_block.Length < o_block_size) {
// create a fullsize block which contains the
// data to encrypt followed by trailing zeros
byte[] x_padded = new byte[o_block_size];
Array.Copy(p_final_block, 0, x_padded, 0, p_final_block.Length);
return ProcessDataBlock(x_padded);
} else {
return ProcessDataBlock(p_final_block);
}
} else {
return new byte[0];
}
}
}
15.3.7 Defining the Decryption Class
The ElGamalDecryptor class extends ElGamalAbstractCipher and is responsible for restoring plaintext using the ElGamal decryption cipher; the DecryptData method in the ElGamalManaged class uses this class:
using System;
public class ElGamalDecryptor : ElGamalAbstractCipher {
public ElGamalDecryptor(ElGamalKeyStruct p_struct) : base(p_struct) {
// set the default block size to be ciphertext
o_block_size = o_ciphertext_blocksize;
}
The ProcessDataBlock method represents the decryption function, and breaks the data block in half to obtain the a and b values that we discussed in the introduction to the ElGamal algorithm; these values are used to compute the plaintext block that is the method return value:
protected override byte[] ProcessDataBlock(byte[] p_block) {
// extract the byte arrays that represent A and B
byte[] x_a_bytes = new byte[o_ciphertext_blocksize / 2];
Array.Copy(p_block, 0, x_a_bytes, 0, x_a_bytes.Length);
byte[] x_b_bytes = new Byte[o_ciphertext_blocksize / 2];
Array.Copy(p_block, x_a_bytes.Length, x_b_bytes, 0, x_b_bytes.Length);
// create big integers from the byte arrays
BigInteger A = new BigInteger(x_a_bytes);
BigInteger B = new BigInteger(x_b_bytes);
// calculate the value M
BigInteger M = (B *
A.modPow(o_key_struct.X, o_key_struct.P).modInverse(o_key_struct.P))
% o_key_struct.P;
// return the result - take care to ensure that we create
// a result which is the correct length
byte[] x_m_bytes = M.getBytes( );
// we may end up with results which are short some leading
// bytes - add these are required
if (x_m_bytes.Length < o_plaintext_blocksize) {
byte[] x_full_result = new byte[o_plaintext_blocksize];
Array.Copy(x_m_bytes, 0, x_full_result,
o_plaintext_blocksize - x_m_bytes.Length, x_m_bytes.Length);
x_m_bytes = x_full_result;
}
return x_m_bytes;
}
The decryption version of the ProcessFinalDataBlock method can assume that there is no partial data to process, because the encryption version will add padding as required:
protected override byte[] ProcessFinalDataBlock(byte[] p_final_block) {
if (p_final_block.Length > 0) {
return ProcessDataBlock(p_final_block);
} else {
return new byte[0];
}
}
}
15.3.8 Testing the Algorithm
The following statements use the smallest supported key size (384 bits) to encrypt and decrypt the string "Programming .NET Security". Export the key parameters from one instance of the ElGamalManaged class and import them into other instances to perform the encryption and decryption:
using System;
using System.Text;
using System.Security.Cryptography;
public class Test {
public static void Main( ) {
// define the byte array that we will use
// as plaintext
byte[] x_plaintext
= Encoding.Default.GetBytes("Programming .NET Security");
// Create an instance of the algorithm and generate some keys
ElGamal x_alg = new ElGamalManaged( );
// set the key size - keep is small to speed up the tests
x_alg.KeySize = 384;
// extract and print the xml string (this will cause
// a new key pair to be generated)
string x_xml_string = x_alg.ToXmlString(true);
Console.WriteLine("\n{0}\n", x_xml_string);
// Test the basic encryption support
ElGamal x_encrypt_alg = new ElGamalManaged( );
// set the keys - note that we export without the
// private parameters since we are encrypting data
x_encrypt_alg.FromXmlString(x_alg.ToXmlString(false));
byte[] x_ciphertext = x_alg.EncryptData(x_plaintext);
// create a new instance of the algorithm to decrypt
ElGamal x_decrypt_alg = new ElGamalManaged( );
// set the keys - note that we export with the
// private parameters since we are decrypting data
x_decrypt_alg.FromXmlString(x_alg.ToXmlString(true));
// restore the plaintext
byte[] x_candidate_plaintext = x_decrypt_alg.DecryptData(x_ciphertext);
Console.WriteLine("BASIC ENCRYPTION: {0}",
CompareArrays(x_plaintext, x_candidate_plaintext));
}
private static bool CompareArrays(byte[] p_arr1, byte[] p_arr2) {
for (int i = 0; i < p_arr1.Length; i++) {
if (p_arr1[i] != p_arr2[i]) {
return false;
}
}
return true;
}
}







