Recipe 5.14 Determining Points Along a Circle
5.14.1 Problem
You want to calculate the coordinates of a point along a circle given the circle's radius and the sweep angle.
5.14.2 Solution
Use the Math.sin( ) and Math.cos( ) methods to calculate the coordinates using basic trigonometric ratios.
5.14.3 Discussion
Finding the coordinates of a point along a circle is easy with some trigonometry. So let's look at the formulas you can use within your ActionScript code and the theory behind them.
Given any point on the Stage?a point we'll call p0, with coordinates (x0, y0)?plus a distance and the angle from the horizontal, you can find the coordinates of another point?which we'll call p1, with coordinates (x1, y1)?using some basic trigonometric ratios. The angle is formed between a conceptual line from p0 to p1 and a line parallel to the X axis, as shown in Figure 5-2. The opposite side (O) is the side furthest away from the angle. The adjacent side (A) is the side that forms the angle with the help of the hypotenuse (H).
Figure 5-2. The angle, adjacent side, opposite side, and hypotenuse of a right triangle
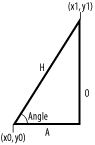
If you know the distance between two points and the angle to the horizontal, as shown in Figure 5-2, you can calculate the x and y coordinates of the destination point using trigonometric functions. The trigonometric sine of the angle is equal to the ratio of the opposite side over the hypotenuse:
sine(angle) = opposite/hypotenuse
Solving for the opposite side's length, this can be written as:
opposite = sine(angle) * hypotenuse
You can see from Figure 5-2 that the opposite side represents the change in the y direction.
The trigonometric cosine of the angle is equal to the ratio of the adjacent side over the hypotenuse:
cosine(angle) = adjacent/hypotenuse
Solving for the adjacent side's length, this can be written as:
adjacent = cosine(angle) * hypotenuse
You can see from Figure 5-2 that the adjacent side represents the change in the x direction.
Because the lengths of the opposite and adjacent sides yield the changes in the x and y directions, by adding the original x and y coordinates to these values you can calculate the coordinates of the new point.
So how does this help in determining a point along a circle's perimeter? Figure 5-3, which shows our familiar triangle inscribed within a circle, emphasizes the equivalency: the triangle's hypotenuse (H) equates to the circle's radius, and the triangle's angle equates to the sweep angle to the point of interest along the circle's perimeter.
Figure 5-3. Using trigonometry to determine a point along a circle's perimeter
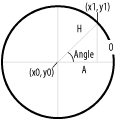
Therefore, the x coordinate of a point along the circle's perimeter is determined by the radius times the cosine of the angle. The y coordinate is determined by the radius times the sine of the angle. Here is the ActionScript code for finding the coordinates of p1 when the circle's radius and center point (p0) are known:
x1 = x0 + (Math.cos(angle) * radius); y1 = y0 + (Math.sin(angle) * radius);
Therefore, these formulas can be used to determine any point along a circle's perimeter, given the circle's center point and radius. By changing the angle over time, you can trace the path of a circle. Here are a few examples:
// Include DrawingMethods.as from Chapter 4.
#include "DrawingMethods.as"
#include "Math.as"
// Create a square_mc movie clip.
_root.createEmptyMovieClip("square_mc", 1);
square_mc.lineStyle(1, 0x000000, 100);
square_mc.drawRectangle(10, 10);
// Move the square in a circular path with a radius of 50. The larger the value by
// which angle is incremented, the faster the movement.
square_mc.onEnterFrame = function ( ) {
this._x = Math.cos(Math.degToRad(this.angle)) * 50;
this._y = Math.sin(Math.degToRad(this.angle)) * 50;
this.angle += 5;
};
// Create another square movie clip.
_root.createEmptyMovieClip("square2_mc", 2);
square2_mc.lineStyle(1, 0x000000, 100);
square2_mc.drawRectangle(10, 10);
// Make the square spiral outward in 30-degree increments, increasing the radius by
// two pixels per frame.
square2.onEnterFrame = function ( ) {
this._x += Math.cos(Math.degToRad(30)) * 2;
this._y += Math.sin(Math.degToRad(30)) * 2;
};
5.14.4 See Also
Recipe 4.5 and Recipe 4.6







